Dijkstra’s algorithm is the most popular algorithm to solve single-source shortest path problems. It can find the shortest path from a given source to all other vertices in a given directed graph. However, it fails to calculate the shortest path correctly in a graph with negative-weighted edges.
For example, consider the following graph with a negative-weighted edge:
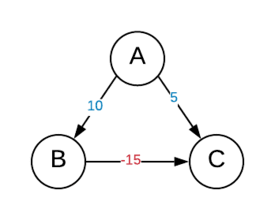
Dijkstra’s algorithm starting from A discovers C and B. In the next step, it visits C and marks it as visited.
Since the vertex is marked visited, the algorithm assumes that the path developed to this vertex (A->C) is the shortest.
But actually, the shortest path from A to C is A->B->C (given that the negative weighted edge has some significance).
Although the given graph didn’t have any negative cycles, the algorithm fails.
In each relaxation step, the algorithm assumes the “cost” to the “closed” nodes is indeed minimal, and thus the node that will next be selected is also minimal.
Stack Overflow
The problem with Dijkstra’s algorithm is that it is believed that all costs in the given graph are non-negative, so adding any positive number on a vertex that has already been visited will never change its minimality.
This problem is well handled by the Bellman-Ford algorithm.
Assuming there are negative edges in the graph, but there are no negative cycles, the Bellman-Ford algorithm iterates through all the edges multiple times (V-1 times), irrespective of the fact whether the vertices are visited or not, thus resulting in successfully finding the optimal low-cost path.
Hope now it’s clear to you, why the Dijkstra algorithm fails to find the right shortest path in a graph with negative weighted edges.