Summary: In this tutorial, we’ll learn what the Bellman-Ford algorithm is, how it works, and how to find the cost of the path from the source vertex to all other vertices in a given graph using the algorithm in C++, Java, and Python.
Introduction to Bellman-Ford Algorithm
Bellman-Ford algorithm is a single source shortest path algorithm that finds the shortest path from the source vertex to all other vertices in a given weighted graph.
For example, if we run the Bellman-Ford algorithm with ‘A’ as the source vertex in the following graph, it will produce the shortest distance from the source vertex to all other vertices of the graph (vertex ‘B’ and ‘C’):
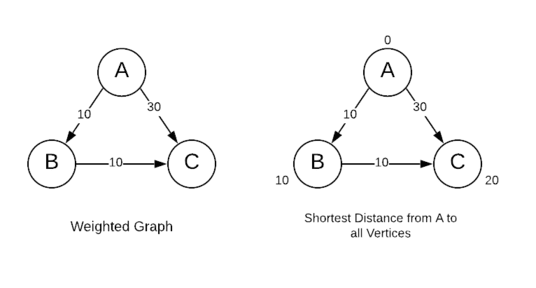
The Belman algorithm works similar to Dijkstra’s algorithm, however, it can handle graphs with negative-weighted edges.
How the Bellman-Ford Algorithm Works?
Bellman-Ford algorithm starts with the initialization process. It initializes the distance of the starting vertex to zero (because the distance from the starting vertex to itself is zero) and all other vertices to positive infinity (∞).
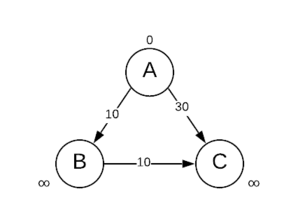
After initialization, the algorithm relaxes all the edges of the graph |V-1| times.
Relaxing means trying to lower the cost of getting to a vertex by using another vertex.
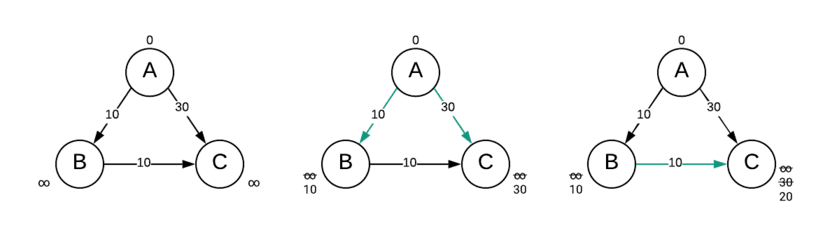
After the relaxation process, the last time the algorithm checks is whether an edge can be further relaxed or not? If yes, the graph has a negative cycle otherwise, the final computed distances on the vertices are the distances from the source vertex to that particular vertex.
Why Each Edge is Relaxed |V-1| Times?
In any given graph, the shortest path between two any two vertices can include a maximum of V vertices (i.e. all the vertices of the graph), and any simple path with a V number of vertices cannot have more than V-1 edges.
Also, like other Dynamic Programming Problems, the Bellman-Ford algorithm finds the shortest paths in a bottom-up manner. It first calculates the shortest distances which have at-most one edge in the path. Then, it calculates the shortest paths with at-most 2 edges, and so on.
Hence, assuming there is no negative cycle in the graph, the Bellman-Ford algorithm treats the search as the worst case and iterates over the edges V-1 times to guarantee the solution.
Implementation of Bellman-Ford Algorithm
Bellman-Ford algorithm in any programming language can be implemented by following the following steps:
- Set the distance of the source vertex to 0 and of all other vertices to +∞.
- Loop |V-1| times.
- Relax all the edges of the graph.
- Try relaxing all the edges one more time.
- If any edge can be relaxed, then it means the given graph has a negative cycle.
- Otherwise, output the distance of the vertices.
Here is the implementation of the algorithm in C++, Java and Python:
Python
class Vertex:
def __init__(self, name):
#vertex label
self.name = name
#distance from the source vertex
self.distance = float('inf')
class Edge:
def __init__(self, _from, _to, _cost):
#from vertex
self._from = _from
#to vertex
self._to = _to
#edge weight or cost
self._cost = _cost
class BellmanFord:
#method implementing Bellman Ford algorithm
def findPath(self, source, edges, v):
#distance of the source vertex to itself is 0
source.distance = 0
#relax all the edges V-1 times
for i in range(v-1):
for edge in edges:
if edge._from.distance + edge._cost < edge._to.distance:
edge._to.distance = edge._from.distance + edge._cost
#If any more relaxation is possible
#then, it means graph has a cycle
for edge in edges:
if edge._from.distance + edge._cost < edge._to.distance:
print("Graph has a negative cycle")
return False
return True
if __name__ == '__main__':
#vertices of the graph
vertices = [Vertex('A'), Vertex('B'), Vertex('C')]
#edges of the graph
edges = [Edge(vertices[0], vertices[1], 10),
Edge(vertices[1], vertices[2], 10),
Edge(vertices[0], vertices[2], 30)]
#driver code
bellmanFord = BellmanFord()
if bellmanFord.findPath(vertices[0], edges, len(vertices)):
#output the distance of the vertices
for vertex in vertices:
print(f"A->{vertex.name}: {vertex.distance}")
C++
#include <iostream>
#include <limits>
#include <list>
using namespace std;
class Vertex{
public:
//vertex label
char name;
//distance from the source vertex
double distance;
Vertex(char name){
this->name = name;
this->distance = numeric_limits<double>::infinity();
}
};
class Edge{
public:
//from vertex
Vertex* from;
//to vertex
Vertex* to;
//edge weight or cost
double cost;
Edge(Vertex *from, Vertex* to, double cost){
this->from = from;
this->to = to;
this->cost = cost;
}
};
class BellmanFord{
public:
//method implementing Bellman Ford algorithm
bool findPath(Vertex* source, list<Edge*> edges, int v){
//distance of the source vertex to itself is 0
source->distance = 0;
//relax all the edges V-1 times
for(int i=1; i<=(v-1); i++){
for(Edge* edge: edges){
if(edge->from->distance + edge->cost < edge->to->distance)
edge->to->distance = edge->from->distance + edge->cost;
}
}
//If any more relaxation is possible
//then, it means graph has a cycle
for(Edge* edge: edges){
if(edge->from->distance + edge->cost < edge->to->distance){
cout << "Graph has a negative cycle";
return false;
}
}
return true;
}
};
int main() {
//vertices of the graph
Vertex* vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C')};
//edges of the graph
list<Edge*> edges {new Edge(vertices[0], vertices[1], 10),
new Edge(vertices[1], vertices[2], 10),
new Edge(vertices[0], vertices[2], 30)};
//driver code
BellmanFord bellmanFord;
if(bellmanFord.findPath(vertices[0], edges, 3))
//output the distance of all the vertex
for(Vertex* vertex: vertices){
cout << "A->" << vertex->name << ": " << vertex->distance << "\n";
}
}Java
import java.util.*;
class Vertex{
//vertex label
char name;
//distance from the source vertex
double distance;
Vertex(char name){
this.name = name;
this.distance = Double.POSITIVE_INFINITY;
}
}
class Edge{
//from vertex
Vertex from;
//to vertex
Vertex to;
//edge weight or cost
double cost;
Edge(Vertex from, Vertex to, double cost){
this.from = from;
this.to = to;
this.cost = cost;
}
}
class BellmanFord{
//method implementing Bellman Ford algorithm
boolean findPath(Vertex source, Edge edges[], int v){
//distance of the source vertex to itself is 0
source.distance = 0;
//relax all the edges V-1 times
for(int i=1; i<=(v-1); i++){
for(Edge edge: edges){
if(edge.from.distance + edge.cost < edge.to.distance)
edge.to.distance = edge.from.distance + edge.cost;
}
}
//If any more relaxation is possible
//then, it means graph has a cycle
for(Edge edge: edges){
if(edge.from.distance + edge.cost < edge.to.distance){
System.out.println("Graph has a negative cycle");
return false;
}
}
return true;
}
}
class Main {
public static void main(String[] args) {
//vertices of the graph
Vertex vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C')};
//edges of the graph
Edge edges[] = {new Edge(vertices[0], vertices[1], 10),
new Edge(vertices[1], vertices[2], 10),
new Edge(vertices[0], vertices[2], 30)};
//driver code
BellmanFord bellmanFord = new BellmanFord();
if(bellmanFord.findPath(vertices[0], edges, 3))
//output the distance of all the vertex
for(Vertex vertex: vertices){
System.out.println("A->"+vertex.name+": "+ vertex.distance);
}
}
}Output:
A->A: 0A->B: 10
A->C: 20
In our example, there were no negative edges in the graph, so we successfully found the distance of each vertex from the source vertex.
Overview of the Bellman-Ford Algorithm
- The Bellman-Ford algorithm|V-1| times relaxes every edge of the graph, hence the time complexity of the algorithm is O(VE).
- Bellman-Ford algorithm can also work with a non-negative undirected graph, but it can only handle negative edges in a directed graph.
- The algorithm often used for detecting negative cycles in a directed graph.
In this tutorial, we learned what the Bellman-Ford algorithm is, how it works, and how to implement Bellman-Ford algorithm in C++, Java, and Python to find the cost of the path.