Summary: In this tutorial, you will learn what is Bubble Sort algorithm and how to sort an array using the Bubble Sort algorithm in C, C++, and Java.
Introduction to Bubble Sort Algorithm
Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order.
Wikipedia
Bubble sort compares two adjacent elements of an array and swaps them if they are in the wrong order.
It repeats this process for each element in the loop until the whole array gets sorted.
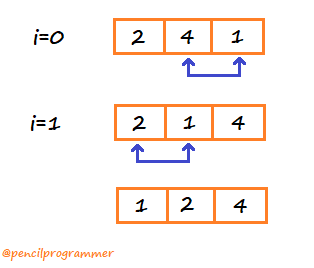
Here, for i=0 iteration, 4 and 1 were found in the wrong order, so they are swapped.
For i=1 iteration, 2 and 1 were found in the wrong order, so this time 2 and 1 are swapped.
For an array of size equal to n, a maximum of n repetition is enough to sort the array using the bubble sort technique.
Bubble Sort Algorithm
for j from 0 to indexOfLastUnsortedElement-1
if array[j] > array[j+1]
swap array[j] and array[j+1]
end Note: This bubble sort algorithm is for sorting an array in ascending order.
After each iteration, the largest element of the unsorted partition gets shifted to the end, so indexOfLastUnsortedElement can be written as sizeOfArray-i, where i is the iteration count.
Here is the implementation of the bubble sort algorithm in C, C++, and Java.
C
#include <stdio.h>
#include <stdlib.h>
void display(int[], int);
int main()
{
int arr[] ={ 2, 6, 1, -5, 3, 10, 0};
int sizeOfArray = sizeof(arr)/sizeof(arr[0]);
int temp;
printf("Unsorted array: ");
display(arr,sizeOfArray);
//Bubble sort
for(int i=0; i< sizeOfArray - 1; i++){
for(int j=0; j<sizeOfArray-i-1; j++){
if(arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
printf("Sorted array: ");
display(arr,sizeOfArray);
return 0;
}
//Function to display array elements
void display(int arr[], int length){
for(int i=0; i<length; i++){
printf("%d ",arr[i]);
}
printf("\n");
}C++
#include <iostream>
using namespace std;
void display(int[], int);
int main()
{
int arr[] ={ 2, 6, 1, -5, 3, 10, 0};
int sizeOfArray = sizeof(arr)/sizeof(arr[0]);
int temp;
cout << "Unsorted array: ";
display(arr,sizeOfArray);
//Bubble sort
for(int i=0; i< sizeOfArray - 1; i++){
for(int j=0; j<sizeOfArray-i-1; j++){
if(arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
cout << "Sorted array: ";
display(arr,sizeOfArray);
return 0;
}
//Function to display array elements
void display(int arr[], int length){
for(int i=0; i<length; i++){
cout<< arr[i] << " ";
}
cout<< endl;
}Java
public class BubbleSort {
public static void main(String args[]){
int i, j, arr[] ={ 2, 6, 1, -5, 3, 10, 0};
int sizeOfArray = arr.length;
int temp;
System.out.print("Unsorted array: ");
display(arr);
//Bubble sort
for(i=0; i< sizeOfArray - 1; i++){
for(j=0; j<sizeOfArray-i-1; j++){
if(arr[j] > arr[j+1]){
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
System.out.print("Sorted array: ");
display(arr);
}
//Function to display array elements
private static void display(int arr[]){
for(int i=0;i<arr.length; i++){
System.out.print(arr[i]+" ");
}
System.out.println();
}
}Output
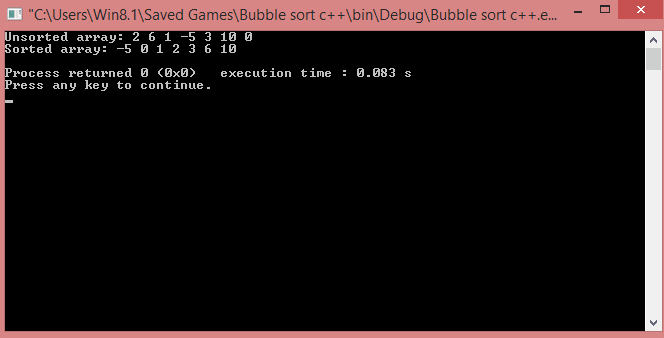
The most important step in the bubble sort is the swapping of the two elements. The code in the program used for swapping element is:
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;Note: In swapping if we would not have stored 1st variable’s value into a temporary location then we could have lost that value on updating it with the 2nd variable’s value.
Bubble Sort Overview
- In place Algorithm – We don’t require an extra array to sort an array.
- O(n²) time complexity – quadratic.
- Becomes insufficient as array sizes grow large.
In this tutorial, we learn’t what is bubble sort algorithm and how to use bubble sort algorithm to sort any liear data structure such as an array.