Convert Binary to Decimal in Java [Loop, Recursion]

Problem: Write a Java Program to convert a binary number into its corresponding decimal representation.

Example:

Input: 101
Output: 5

Input: 1111
Output: 15

Method 1: Using While Loop

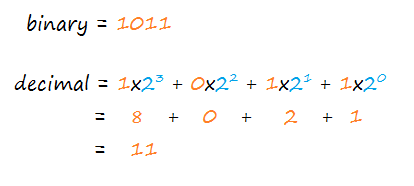
To convert a binary into a decimal we multiply the digits of the binary with their respective exponential value of 2 (2^{position from right – 1}) and sum them up.

To iterate through the digits in Java, we use the while loop as follows:

import java.util.Scanner;
 
public class Main
{
	public static void main(String[] args) {
	    Scanner in=new Scanner(System.in);
	    int lastDigit, decimal=0, i=0;
	    
	    //Input binary number
		System.out.println("Enter a Binary");
		int binary = in.nextInt();
		
		
		while(binary>0){
		    //extract digit
		    lastDigit = binary%10;
		    
		    //multiply digit with the 2^i and add to the sum
		    decimal += Math.pow(2,i) * lastDigit;
		    
		    //update binary by removing the last digit
		    binary = binary/10;      
		    
		    i++;    //Increment exponent ('i')
		}
		
		//output decimal
		System.out.println("Decimal: "+decimal);
	}
}

Output:

Enter a Binary: 101
Decimal: 5

Method 2: Using Recursion

The approach used in this method is the same as the above but implemented in a recursive fashion.

On every recursive call, we extract the last digit, multiply it with its corresponding exponential value of 2 and return its sum with the next recursive call result.

import java.util.Scanner;
 
public class Main
{
	public static void main(String[] args) {
	    Scanner in=new Scanner(System.in);
	    
	    //Input the binary number
		System.out.println("Enter a Binary");
		int binary = in.nextInt();
		
		//pass the binary number to the recursive function
		//and print the result returned
		System.out.println("Decimal: "+binToDec(binary, 0));
	}
	
	//'i' represents the nth recursive call as well as
    //nth digit from left, so it can be used as an exponent
    private static int binToDec(int bin, int i){
        //base condition
        if(bin == 0 || bin == 1)
            return (int)Math.pow(2,i)*bin;
        
        //extract digit
        int lastDigit = bin%10;
        
        //return the arithemetic result with next recusive call
        return (int)(Math.pow(2,i) * lastDigit) + binToDec(bin/10, ++i);
     
    }
}

Output:

Enter a Binary: 1111
Decimal: 15

It is important to note that on every next recursive call, we are eliminating the last digit from the binary number that has been processed in the current recursion.

If you have any doubts or suggestions then below.