Convert Decimal to Binary in Java [Loop, Recursion]

Problem: Write a Java Program to convert a decimal number into its binary representation.

Example:

Input: 5
Output: 101

Input: 2
Output: 10

To achieve the remainder in the bottom-up manner we need to concatenate each of the upcoming remainders to the left of the concatenated binary number. For this, we will need to first multiply equal number 10 to the remainder as the number of digits already present in the concatenated binary number and then add to the concatenated binary number.

Method 1: Using While Loop

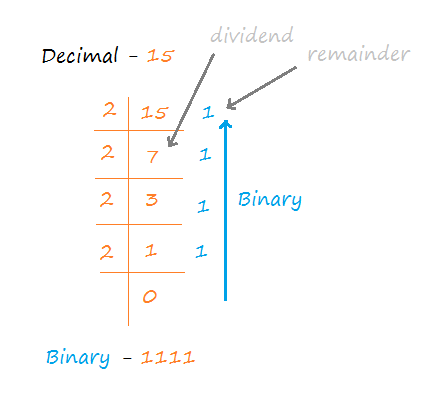
To convert decimal into binary, we divide the decimal number by 2 until it reduces to 0.

The bottom-up sequence of the remainders that we get after division is the binary representation of the corresponding decimal number.

In Java, we use implement the same using a while loop as follows:

import java.util.Scanner;
 
public class Main
{
	public static void main(String[] args) {
	    Scanner in= new Scanner(System.in);
	    int i=1, binary=0, rem;
	    
	    //Enter the decimal number
		System.out.println("Enter a number");
		int num = in.nextInt();
		
		//Divide by 2 until number reduces to 0
		while(num!=0){
		    rem = num%2;
		    binary += i*rem;    //concatenate remainders in bottom-up manner
		    num = num/2;
		    i=i*10;
		}
		
		//Output the binary number
		System.out.println("Binary: "+ binary);
	}
}

Output:

Enter a number
5
Binary: 101

Method 2: Using Recursion

The logic to convert a decimal into binary is same as the above method, but is implemented using recursion.

import java.util.Scanner;
 
public class Main
{
	public static void main(String[] args) {
	    Scanner in= new Scanner(System.in);
	    
	    //Enter the decimal number
		System.out.println("Enter a number");
		int num = in.nextInt();
		
		//Call the decToBin() recursive function to print binary equivalent
		System.out.print("Binary: ");
		decToBin(num);
	}
	
	//recursive method
	private static void decToBin(int n){
        //divide until number reduces to 0
        if(n > 0){
            decToBin(n/2);            //recursive call with quotient
            System.out.print(n%2);    //print remainder
        }
    }
}

Output:

Enter a number
15
Binary: 1111

In this method, we pass the quotient of the current division to the next recursive call. We do this until the passed number is reduced to zero.

The important part of the recursive function is the print statement. In the print statement, we are printing the remainder of the current division, which is written after the recursive call.

Because of this, the remainders start printing from the last recursive call, so gets printed in a bottom-up manner (resulting binary).