Solve Tower of Hanoi using Recursion in Java

Summary: In this programming example, we will learn to solve the Tower of Hanoi problem using recursion in Java.

What is the Tower of Hanoi?

Tower of Hanoi is a game of rods and discs that requires a certain number of discs of different sizes to be transferred from one rod to another.

The simple tower of Hanoi Puzzle includes 3 rods and 3 discs in ascending order, with the smallest one on top.

Our aim is to move all disks to the destination tower in the same order by following the following rules:

• One disk should be moved at a time.
• A large disk should not be placed on top of a smaller disk.

Initially, we have this stack:

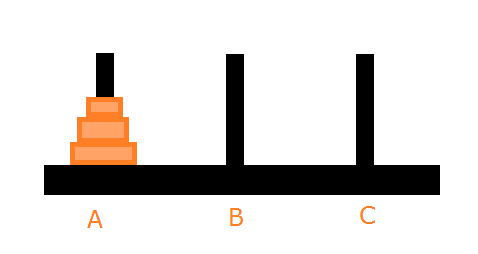
We want to achieve this stack to solve the puzzle.

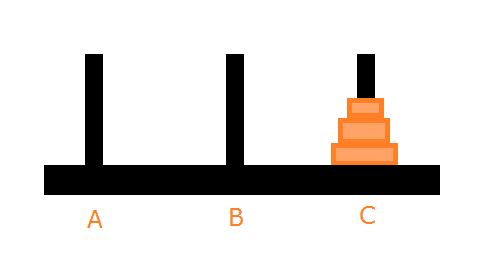
To solve the Tower of Hanoi problem, we will use recursion because every subset of the discs is itself a tower of Hanoi problem.

The Tower of Hanoi can have many problems depending on the number of discs, in our example we will solve Hanoi’s 3 disc tower for the demonstration purpose.

Tower of Hanoi Solution using Recursion

The trick is to assume that we are given only two disks (as stated in the picture).

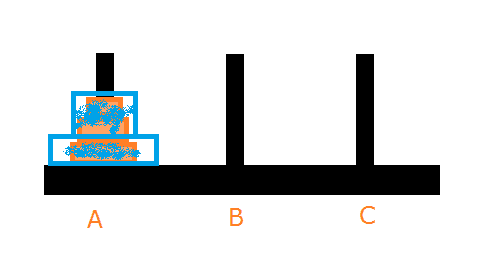
Now we need to shift the upper disc i.e. n-1 (2 discs in the current scenario) to B so that we can shift the last disk (n-th) to C.

The main point is we will not do this. The recursive function will take the responsibility to shift n-1 disks (2 disks in this case) to B.

hanoi(n-1, rodFrom, rodTo, rodMiddle)

where rodFrom = A , rodTo = B and rodMiddle = C.

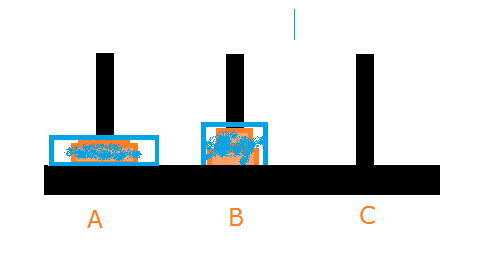
Now we have to shift the last disk (n^th or the largest disc) to rod C. So we will do this by printing the statement as follows:

System.out.println("Disk "+n+" moved from "+rodFrom+" to "+rodTo)

where n=3, rodFrom = A and rodTo = C .

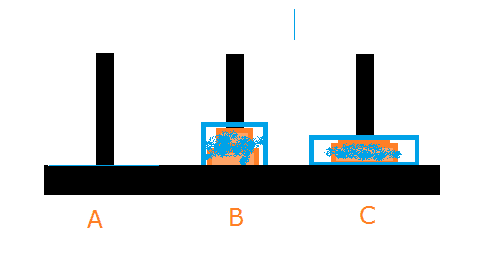
Now again the n-1 discs (2 discs in rod B) need to be shifted to rod C with the help of rod A.

Since there are multiple risks involved in this turn, let the recursive function handle this task.

hanoi(n-1, rodMiddle, rodFrom, rodTo)

where rodFrom = B , rodTo = C and rodMiddle = A will be used as auxiliary rod by the recursive function.

Finally, we will get this i.e Tower of Hanoi solved.

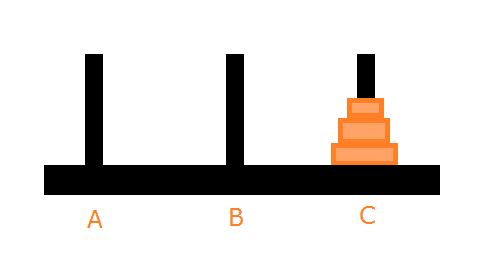
Here is the full source code in Java that solves the Tower of Hanoi problem as discussed above.

class Main {
 
  public static void main(String[] args) {
    hanoi(3, 'A', 'B', 'C');
  }
 
  private static void hanoi(int n, char rodFrom, char rodMiddle, char rodTo){
 
    if(n==1){
      System.out.println("Disk 1 moved from "+rodFrom+" to "+rodTo);
      return;
    }
 
    //Move top n-1 disks from A to B using C as middle
    hanoi(n-1,rodFrom,rodTo,rodMiddle);
 
    //Move last disk from A to C
    System.out.println("Disk "+n+" moved from "+rodFrom+" to "+rodTo);
 
    //Move n-1 disks from B to C using A as middle
    hanoi(n-1,rodMiddle,rodFrom,rodTo);
 
  }
}

Output:

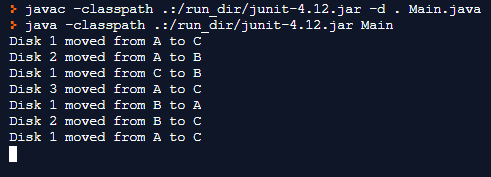
In this programming example, we have solved the tower of hanoi problem using the Java programming language.