Summary: In this tutorial, we will learn what is Breadth First Search Algorithm and how to use the BFS algorithm to traverse graphs or trees in C++ and Java.
Introduction to Breadth First Search Algorithm
Breadth-first search is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
Wikipedia
In breadth-first search, the neighbour nodes are traversed first before the child nodes.
For example consider the following GIF visualizing the BFS tree traversal:
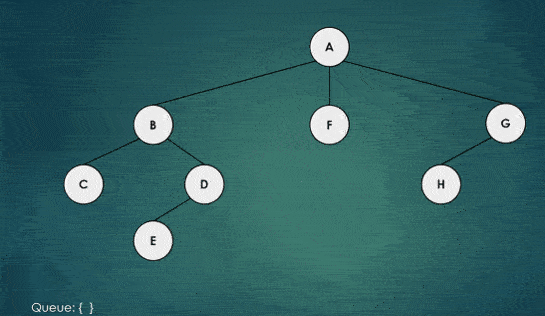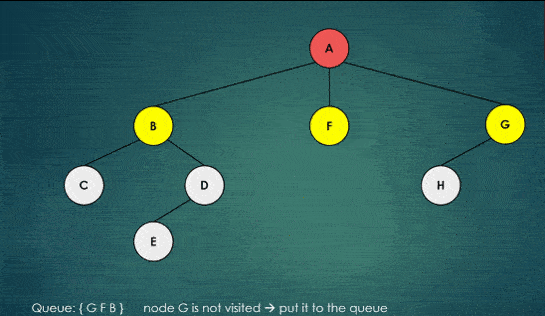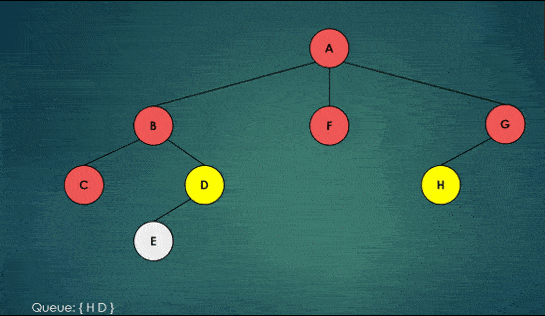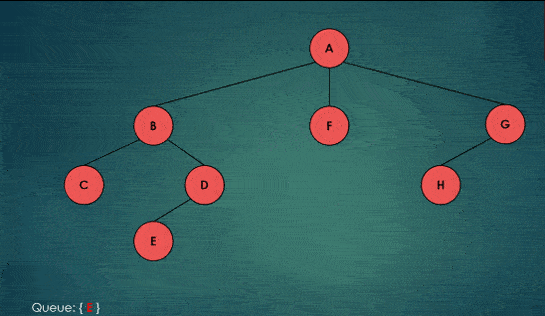
Yellow color: Node added to the queue for the next visit. Red color: Node marked visited and removed from the queue.
As you can notice, the breadth-first search algorithm is visiting all the nodes in the current depth before moving to the next depth level.
The technique used in BFS is the opposite of DFS. DFS explores all nodes along a branch until the leaf node and backtracks to visit nodes of other branches.
How Breadth-First Search Works?
BFS uses queue to traverse nodes or vertex of a graph or tree.
BFS first pushes all neighbor nodes of the current depth into the queue and then visits them by following the FIFO (First In First Out) pattern.
While visiting a node, BFS simultaneously adds its unvisited neighbors to the queue.
Since the queue follows the FIFO pattern, the vertex at the highest level is popped and visited first.
More is the depth of the nodes later it will be processed by the queue, hence implementing breadth-first search traversal.
Breadth-First Search Algorithm
The algorithm for breadth-first search traversal is:
- Select the root of the graph.
- Insert the root vertex into the queue.
- Pop a vertex from the queue, mark it as visited, and output its value.
- Visit its unvisited neighbor vertex, push them to the queue, and mark visited.
- Repeat step 3 until the queue is empty.
- When the queue is empty, end the program.
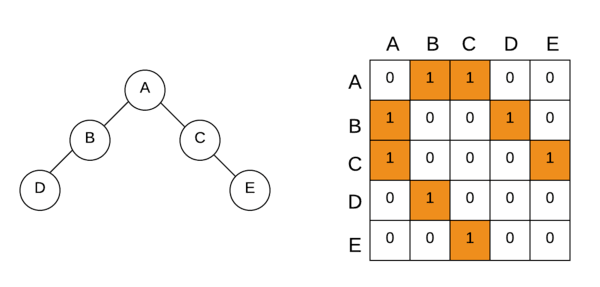
Breadth First Search using Adjacency Matrix
The adjacency matrix is a 2D array that maps the connections between each vertex.
if adjancyM[2][3] = 1, means vertex 2 and 3 are connected otherwise not.
Here is the corresponding adjacency matrix of the graph that we have used in our program:
Here is the implementation of breadth first search algorithm using adjacency matrix:
C++
#include <iostream>
#include <queue>
#define SIZE 5
using namespace std;
//vertices
char vertices[SIZE] = {'A', 'B', 'C', 'D', 'E'};
//array mapping to mark visited vertices
int visited[SIZE] = {0};
//Adjacency Matrix (Graph)
int adjacencyM[SIZE][SIZE] = {{0, 1, 1, 0, 0},
{1, 0, 0, 1, 0},
{1, 0, 0, 0, 1},
{0, 1, 0 ,0, 0},
{0, 1, 1, 0, 0}};
class BFS{
public:
void solve(int root){
queue<int> Queue;
//Visit root node and add to the queue
visited[root] = 1;
Queue.push(root);
//BFS until queue is empty
while(!Queue.empty()){
//Pop the vertex and display
int current_vertex= Queue.front();
Queue.pop();
cout << vertices[current_vertex] << " ";
//add connected non-visited vertices to the queue
int neighbor_Vertex;
while((neighbor_Vertex =unvisitedNeighbor(current_vertex)) != -1){
//Mark neighbors as visited
visited[neighbor_Vertex] = 1;
Queue.push(neighbor_Vertex);
}
}
}
//Function returns index of unvisited connected vertices
int unvisitedNeighbor(int index){
for(int i=0; i<SIZE; i++){
if(adjacencyM[index][i] == 1 && (visited[i] == 0)){
return i;
}
}
return -1;
}
};
//Driver Code
int main() {
BFS bfs;
bfs.solve(0);
return 0;
}Java
import java.util.LinkedList;
import java.util.Queue;
class BFS{
int adjacencyM[][];
char vertices[];
int visited[];
BFS(int adjacencyM[][], char[] vertices){
this.adjacencyM = adjacencyM;
this.vertices = vertices;
this.visited = new int[vertices.length];
}
public void solve(int root){
//Visit root vertex and add to the queue
Queue<Integer> queue = new LinkedList<>();
queue.add(root);
visited[root] = 1;
while(!queue.isEmpty()){
//Pop and display the vertex from queue
int current_vertex = queue.poll();
System.out.print(vertices[current_vertex]+" ");
//Visit and add all unvisited neighbors to the queue
int v;
while((v =unvisitedNeighbor(current_vertex)) != -1){
queue.add(v);
visited[v] = 1;
}
}
}
//Function returns index of unvisited connected vertices
private int unvisitedNeighbor(int index){
for(int i=0; i<adjacencyM.length; i++){
if(adjacencyM[index][i] == 1 && visited[i] == 0){
return i;
}
}
return -1;
}
}
class Main {
public static void main(String[] args) {
//vertices
char vertices[] = {'A', 'B', 'C', 'D', 'E'};
//Adjacency Matrix
int adjacencyM[][] = {{0, 1, 1, 0, 0},
{1, 0, 0, 1, 0},
{1, 0, 0, 0, 1},
{0, 1, 0 ,0, 0},
{0, 1, 1, 0, 0}};
BFS bfs = new BFS(adjacencyM,vertices);
bfs.solve(0);
}
}Output:
A B C D EBreadth First Search using Adjacency List
Each node or vertex holds the list of its neighbor’s nodes known as the Adjacency List.
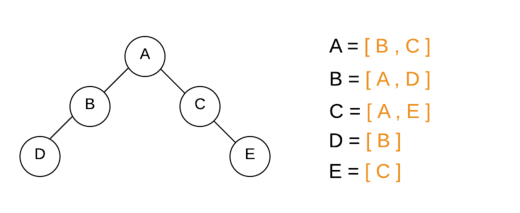
In the following program, instead of an adjacency matrix, we have implemented the BFS algorithm using the adjacency list:
C++
#include <iostream>
#include <queue>
#include<list>
using namespace std;
class Vertex{
public:
//Adjacency List of the vertex
list<Vertex*> neighbors;
char name ;
bool visited = false;
Vertex(){}
Vertex(char name){ this->name = name;}
//Method to connect vertices
void addNeighbour(Vertex* v){
this->neighbors.push_back(v);
v->neighbors.push_back(this);
}
};
class BFS{
public:
void bfs(Vertex* root){
//Visit Root vertex and add to queue
root->visited = true;
queue<Vertex*> Queue;
Queue.push(root);
//BFS until queue is empty
while(!Queue.empty()){
//Pop a vertex and display
Vertex* current_vertex=Queue.front();
Queue.pop();
cout << current_vertex->name << " ";
//Loop through neighbors vertices
for(Vertex* v: current_vertex->neighbors){
if(!v->visited){
//Visit and add neighbor vertices to the queue
v->visited= true;
Queue.push(v);
}
}
}
}
};
int main()
{
//create vertices
Vertex v1('A'), v2('B'), v3('C'), v4('D'), v5('E');
//connect vertices
v1.addNeighbour(&v2);
v1.addNeighbour(&v3);
v2.addNeighbour(&v4);
v3.addNeighbour(&v5);
//Driver Code
BFS b;
b.bfs(&v1);
}Java
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.ArrayList;
class Vertex {
//Adjacency List
List<Vertex> neighbors = new ArrayList<>();
char data;
boolean visited = false;
Vertex(char ch){
this.data = ch;
this.visited = false;
}
//Method to connect vertices
void addNeighbor(Vertex v){
this.neighbors.add(v);
v.neighbors.add(this);
}
}
class BFS {
public void solve(Vertex root){
Queue<Vertex> queue = new LinkedList<>();
//Visit root node and add to queue
root.visited = true;
queue.add(root);
//BFS until queue is empty
while(!queue.isEmpty()){
//Pop from queue and display the node
Vertex current_vertex = queue.poll();
System.out.print(current_vertex.data+" ");
//Loop through neighbor nodes
for(Vertex v:current_vertex.neighbors){
if(!v.visited){
//Visit and add to the queue
v.visited = true;
queue.add(v);
}
}
}
}
}
class Main{
public static void main(String args[]){
//Creating vertices
Vertex v1 = new Vertex('A');
Vertex v2 = new Vertex('B');
Vertex v3 = new Vertex('C');
Vertex v4 = new Vertex('D');
Vertex v5 = new Vertex('E');
//connecting vertices
v1.addNeighbor(v2);
v1.addNeighbor(v3);
v2.addNeighbor(v4);
v3.addNeighbor(v5);
//Driver code
BFS b = new BFS();
b.solve(v1);
}
}Note: The use of pointers is necessary, otherwise the object’s copy will be created and changes in the visited value of vertex will not be reflected, causing infinite iteration.
Output:
A B C D EBreadth-First Search Overview
- The time complexity of the BFS algorithm is equivalent to O(V+E), where V is the number of the vertices and E is the number of edges of the graph.
- Breadth-First Traversal is also known as Level Order Traversal.
- BFS is often used for GPS navigations, finding paths, cycle detection, etc.
In this tutorial, we learned what is the breadth-first search algorithm and how to implement the BFS algorithm to traverse a graph or tree using the adjacency list and adjacency matrix in C++ and Java.