Summary: In this tutorial, we will learn what is Depth First Search and how to traverse a graph or tree using Depth First Search in C, C++, and Java.
Introduction to Depth First Search
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
Wikipedia
DFS starts from the root node (or any arbitrary node as the root node) and explores as far as possible along each branch in depth before backtracking.
The following diagram illustrate depth first search traversal of a tree.
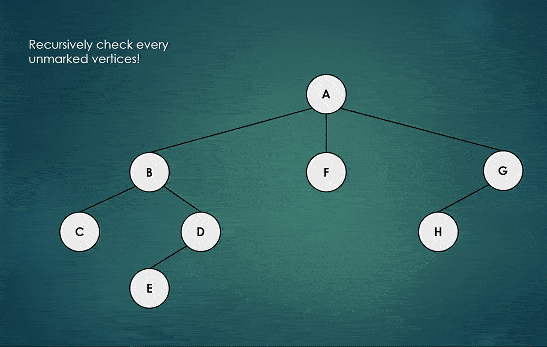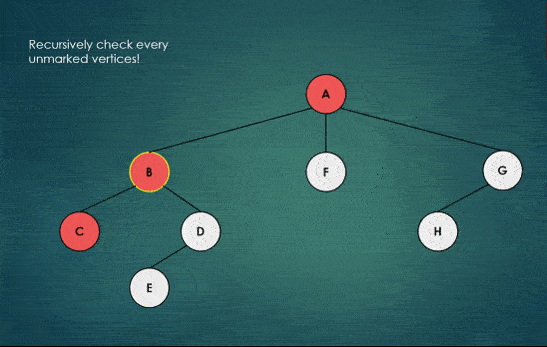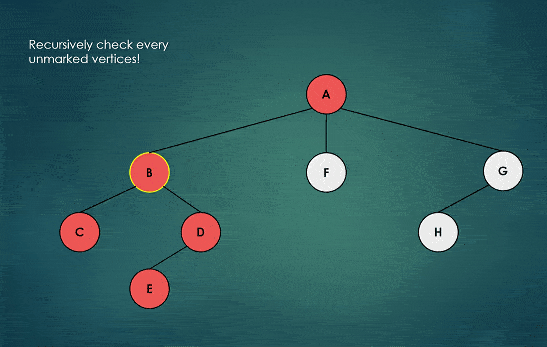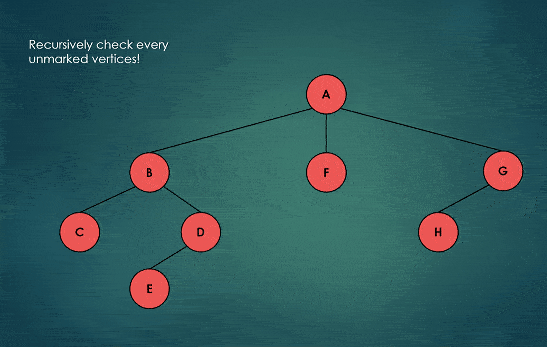
The red color indicates visited nodes, while the yellow circle movement is illustrating the backtracking process.
DFS algorithm uses stack to keep track of the visited nodes.
We add the visited node to the stack during the process of exploring the depth and use it to traverse back to the root node or any other sub-root node for the need of exploring the next unvisited branch.
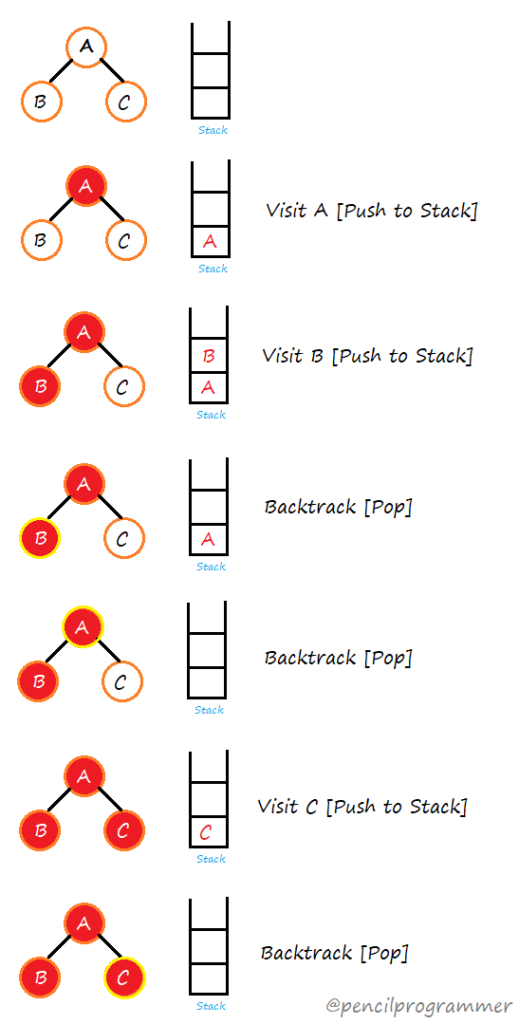
Although we can use an explicit stack to store visited nodes, it is recommended to use recursion to implement DFS because recursion easily implements backtracking
Here is the DFS algorithm that describes the process of traversing any graph or tree.
Depth First Search Algorithm
- Visit the root node.
- Check if the root has any neighbor/child. If yes then visit the child.
- Check whether the current node has any neighbor/child. If yes then visit its child.
- Repeat the process (Step 3) until you reach the node which does not have any child i.e. leaf node.
- At the leaf node traverse back 1 level to its parent node and check if it has any child unvisited. If yes then visit the node and repeat step 3 for this node. If not then go back 1 level i.e. repeat step 4.
- End if all nodes are visited.
Here is the implementation of the DFS algorithm in C, C++, and Java.
C
#include <stdio.h>
#include <stdlib.h>
#define MAX 10
//DFS using Adjacency Matrix
int i, visited[MAX];
char vertex[MAX];
//adjacency matrix
int graph[MAX][MAX] = {{0,1,0,1,0},
{1,0,1,0,0},
{0,1,0,0,0},
{1,0,0,0,1},
{0,0,0,1,0}};
void dfs(int currentVertex){
printf("%c ",vertex[currentVertex]);
visited[currentVertex] = 1;
for(i=0; i<MAX; i++ ){
if(visited[i] == 0){
//Recursive calling dfs() i.e implementing stack
dfs(i);
}
}
}
int main()
{
//Adding vertex to the graph
vertex[0] = 'A';
vertex[1] = 'B';
vertex[2] = 'C';
vertex[3] = 'D';
vertex[4] = 'E';
//Assuming Vertex A as root
dfs(0);
return 0;
}C++
#include <iostream>
#include <list>
#include <stack>
#include <iterator>
#define Max 10 ;
using namespace std;
//Vertex class
class Vertex{
public:
list<Vertex*> neighbors;
char name;
bool visited;
Vertex(): name{'\0'},visited{false}{}
Vertex(char ch): name{ch},visited{false}{}
void addNeighbor(Vertex *v){
neighbors.push_back(v);
}
};
class DFS{
public:
void dfs(Vertex *currentVertex){
cout << currentVertex->name <<" ";
list<Vertex*> nbr = currentVertex->neighbors;
//Iterating through each neighbor
list<Vertex*> :: iterator it;
for(it=nbr.begin(); it != nbr.end();it++ ){
if(!(*it)->visited){
(*it)->visited = true;
//Recursive calling dfs() i.e implementing stack
dfs(*it);
}
}
}
};
int main()
{
//Adding vertex to the graph
Vertex v1('A'), v2('B'),v3('C'),v4('D'),v5('E');
//Connecting vertex OR assigning neighbor
v1.addNeighbor(&v2);
v1.addNeighbor(&v4);
v4.addNeighbor(&v5);
v2.addNeighbor(&v3);
DFS b;
//Assuming Vertex v1 as root
b.dfs(&v1);
return 0;
}Java
import java.util.ArrayList;
import java.util.List;
class Vertex{
char value;
List<Vertex> adVertex;
boolean visited;
Vertex(char value){
this.value =value;
adVertex = new ArrayList<>();
visited = false;
}
public void addAdVertex(Vertex v){
//Bidirectional edge (this <---> v)
this.adVertex.add(v);
v.adVertex.add(this);
}
public void display(){
System.out.print(this.value+" ");
}
}
class DFS{
public void solve(Vertex root){
root.visited = true;
root.display();
for(Vertex v: root.adVertex){
//If unvisited go depth recursively
//otherwise move to next adjacent vertex
if(!v.visited){
solve(v);
}
}
}
}
class Main {
public static void main(String[] args) {
DFS dfs = new DFS();
//Create Vertices
Vertex vertexA = new Vertex('A');
Vertex vertexB = new Vertex('B');
Vertex vertexC = new Vertex('C');
Vertex vertexD = new Vertex('D');
Vertex vertexE = new Vertex('E');
//Join vertices
vertexA.addAdVertex(vertexB);
vertexA.addAdVertex(vertexD);
vertexB.addAdVertex(vertexC);
vertexD.addAdVertex(vertexE);
//call solve() method
dfs.solve(vertexA);
}
}The tree connection which we have used in the program:
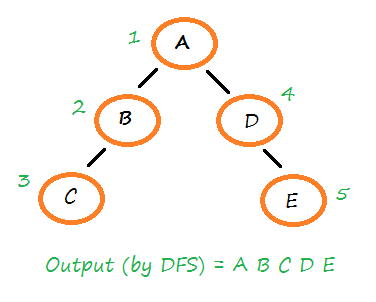
Output of Program
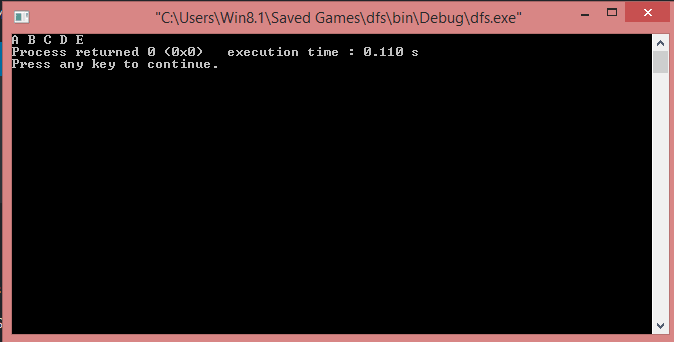
Note: In this tutorial, we are assuming that the graph is connected. For the unconnected graph, this code will give unwanted output.
In this tutorial, we learned Depth First Seach and its implementation in C, C++, and Java. Check out Breadth-first search tutorial if you haven’t.