Summary: In this tutorial, we will learn what is Backtracking and how to use the Backtracking algorithm to find solutions to some computational problems.
What is Backtracking Algorithm?
To understand backtracking, consider the following situation:
Imagine, you want to go from one city to another by driving. There are many routes to your destination city and you choose one of them.
In the way, you found a road is undergoing construction or is closed.
What will you do?
Definitely you will not go back straight away to your home to take another route. You return to the last turn to take other available free roads to continue your journey.
This process of going back a little and continuing with another valid path is known as Backtracking.
In short, Backtracking Algorithm is simply, going one step back to proceed with the next available option when no further solution is possible.
Graphical Representation of Backtracking
Graphically, Backtracking appears to be Depth First Search because DFS implements backtracking.
Observe the animation below, you will notice that on reaching the end (i.e leaf node), we go back upwards one step and check if there is some child node unvisited. we visit that node (i.e follow the new node’s path).
We repeat this process until we visit all the nodes of the graph.
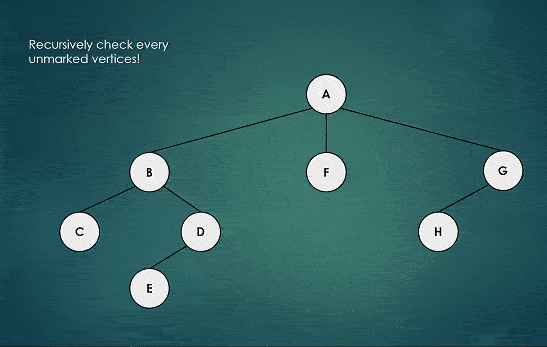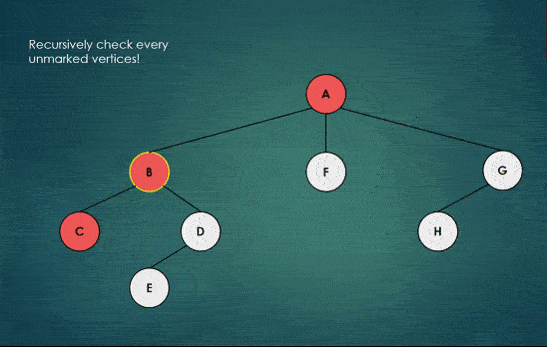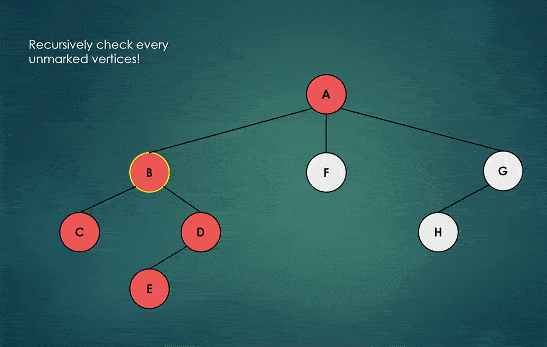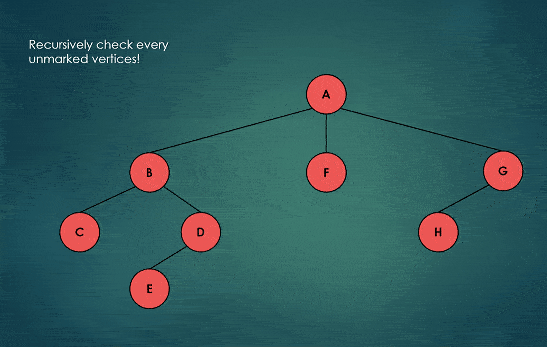
Note: Depth First Search means, first go to the depth along a single path/branch unless no option is left, then come back by checking the chances of going forward at each step.
How to implement Backtracking?
Backtracking is implemented using a stack.
In Backtracking, we require to go back on reaching a particular point or situation and for this, we need to keep track of what we have processed in previous steps. Therefore stack which follows the LIFO (Last In First Out) pattern helps in accomplishing the same.
In order to implement a stack, we use Recursion. Because in Recursion, on reaching the base case the recursive function traces back the previous recursive calls.
Simultaneously in the process of backtracking, we explicitly manipulate recursive function so that it goes forward with a different option if available.
Here is the code snippet of Depth First Search implementing Backtracking.
void dfs(int currentNode){
printf("%c ",vertex[currentNode]);
visited[currentNode] = 1;
// i decides the next path (node)
for(i=0; i<MAX; i++ ){
if(visited[i] == 0){
//Recursive call
dfs(i);
}
}
}Refer this post for full Depth First Search Program.
How to know When to Use Backtracking?
Anytime you solve a problem, that is solved by a series of decisions, you might make a wrong decision and when you realize that, you have to backtrack to a place where you made a decision and try something else.
Thus, break and analyze your given problem. If the series of decisions need to be made in the process to solve your problem, then there is a high chance, that the problem can be solved using Backtracking.
Example: N Queens Problem
In ‘N Queens Problem’, we require to decide for every chessboard cell, whether it is safe to place queen or not. If yes then we proceed to the next column for another queen, else we go back to decide another safe cell to place previously placed queen.
Backtracking Overview
- Backtracking is often much faster then Brute Force method because it can eliminate large number of decisions with a single test.
- Backtracking is an important tool for solving constraint satisfaction problem.
- The Backtacking algorithm traverses the tree recusively from the root to down(DFS).
- Soduko can be solved using Backtracking
Implementation of the Backtracking algorithm for different types of problems can vary drastically. Hence writing general pseudocode for backtracking is not a wise move. First, understand the concept of backtracking and try to implement it with the use of recursion.
Do check our different examples on the backtracking algorithm here to know how to use Backtracking.
In this tutorial, we learned the concept of Backtracking algorithm with examples and also got to know how to implement backtracking algorithm using recursion.