Summary: In this tutorial, we will learn what N Queen Problem is and how to solve N Queen Problem using the Backtracking algorithm in C and Java.
What is N Queen Problem?
We are given N chess’s queens and asked to place them in the chessboard of size NxN so that no two queens attack/eliminate each other.
A queen can only attack if another queen is either on:
- Same Row
- Same Column
- Same Diagonal (left or right)
Example: For the 4 Queens problem, we have a 4×4 board. If a queen is placed at (2,2), then the places where no queen should be placed are crossed by the red lines as shown in the figure:
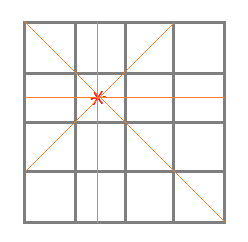
Solution for N Queen Problem
Now the question is how to solve N Queen Problem?
There are two approaches to solve this problem:
Naïve Algorithm
In this approach, we use the brute force method by randomly choosing the position to find all possible solutions.
while some configurations are unchecked
{
Generate configuration of queen position
if in current configuration queens don't attack
{
print the configuration
}
}This approach is not efficient because it test all possible configuration which repeats same queens placements repeatedly.
Backtracking Algorithm
In this approach, we place a queen in one column, and then we proceed to the next column (since a single column cannot contain more than one queen).
We then check the possible safe row position to place the next queen, so that we can proceed to the next column.
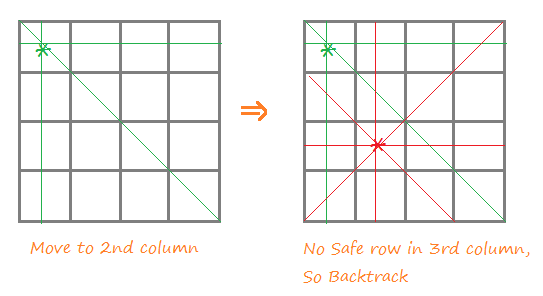
If there is no safe row in the current column, we go back to the previous column and change the queen’s position to the next possible safe row position. If have any, we proceed to the next column again, else we go back further and repeat the same task.
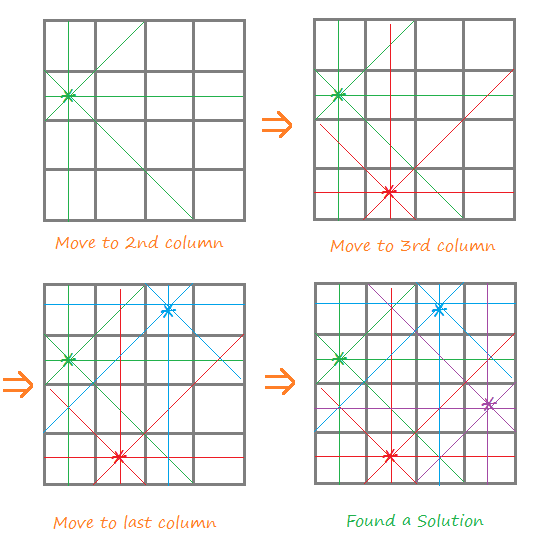
If we reached the last column and found the possible safe position (i.e. row), we print the configuration of queens (i.e. solution), else if we came back to the first column and none of the position (i.e. row) is safe then we assume that there is no possible solution.
So, In backtracking, if no further solution is possible, we go one step back and proceed with next available option.
Check N-Queens Visualizer to get visual working of backtrack algorithm.
find_solution(row, column)
{
if (column == lastColumn + 1)
{
passed all columns, therefore successfully found a solution;
print board;
return true;
}
else
{
for(all rows of column)
{
if([row, column] is safe for placing queen)
{
//place queen, i.e
board[row][column] = 1;
//check for next column
if(find_solution(0,column + 1))
{
return true;
}
//No safe place in column+1, remove queen, i.e
board[row][column] = 0;
}
move to next row
}
checked all rows of the column, no safe place;
return false;
}
}Here is the implementation of the algorithm in C and Java:
C
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
void solveColumn(int);
bool isValidPlace(int , int);
void displayBoard();
void solveNqueen();
//global variables
int queens;
int chessBoard[20][20];
bool hasSolution = false;
int main(){
//enter value of N (i.e. number of coulmns)
printf("Enter number of Queens: ");
scanf("%d", &queens);
//call the method to start solving the N queen
solveNqueen();
return 0;
}
void solveNqueen(){
/* the solveColumn(int) is a recursive function,
that checks and place the queens column wise.
So, initate the solving from the 1st column */
solveColumn(0);
/* though the solveColumn(int) outputs the possible solutions,
but if no solution was found, output "No Soultion" message. */
if(!hasSolution)
printf("No Solution \n");
}
//recursive backtracking method
void solveColumn(int col){
/* if reached beyond the last column, means
a solution (configuration) has been found*/
if(col == queens){
hasSolution = true;
/* display the board configuration and
return to find more possible solution */
displayBoard();
return;
}
//loop through the column
for(int i=0; i<queens; i++){
//checking if the current cell is safe to place a queen
if(isValidPlace(i,col)){
//setting current value to 1 means placing a queen
chessBoard[i][col] = 1;
//moving to next column's 1st row
solveColumn(col+1);
//backtrack - reset to 0 means removing queen
chessBoard[i][col] = 0;
}
}
}
//function checks whether the position is safe or not
bool isValidPlace(int row, int col){
//Check horizontally
for(int i=col; i>=0; i--){
if(chessBoard[row][i] == 1)
return false;
}
//check the left diagonal
for(int i=row, j=col; i>=0 && j>=0; i--,j--){
if(chessBoard[i][j] == 1)
return false;
}
//check the right diagonal
for(int i=row, j=col; i<queens && j>=0; i++,j--){
if(chessBoard[i][j] == 1)
return false;
}
//return true because it is safe
return true;
}
//funtion to display the board
void displayBoard(){
for(int i=0; i<queens; i++){
for(int j=0; j<queens; j++){
if(chessBoard[i][j] == 1)
printf(" * ");
else
printf(" - ");
}
printf("\n");
}
printf("\n \n");
}Java
import java.util.*;
class Main {
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
//Enter the value of N (i.e. the number of columns/queens)
System.out.print("Enter Queens: ");
int n = in.nextInt();
//create the object of NQueen class and call the solve() method
NQueen nQueen = new NQueen(n);
nQueen.solve();
}
}
class NQueen{
int n;
int board[][];
boolean hasSolution = false;
//constructor takes N as a parameter
NQueen(int n){
this.n = n;
board = new int[n][n];
}
//function display the board configurations
private void printBoard(){
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(board[i][j] == 1)
System.out.print("* ");
else
System.out.print("- ");
}
System.out.println();
}
System.out.println("\n");
}
public void solve(){
/* the solveColumn(int) is a recursive function,
that checks and place the queens column wise.
So, initate the solving from the 1st column */
solveColumn(0);
/* though the solveColumn(int) outputs the possible solutions,
but if no solution was found, output "No Soultion" message. */
if(!hasSolution)
System.out.println("No Solution");
}
//recursive backtracking method
private void solveColumn(int col){
/* if reached beyond the last column, means
a solution (configuration) has been found*/
if(col == n){
hasSolution= true;
/* display the board configuration and
return to find more possible solution */
printBoard();
return;
}
//loop through the current column cells
for(int i=0; i<n; i++){
//check if the current cell is safe to place a queen
if(isValidPlace(i,col)){
//if yes then place the queen - change value to 1 and
//move to the next column
board[i][col] = 1;
solveColumn(col+1);
//backtrack - reset to 0 means removing queen
board[i][col] = 0;
}
}
}
//function checks if the position (r,c) is safe
private boolean isValidPlace(int r, int c){
//Check horizontally (left)
for(int j=c; j>=0; j--){
if(board[r][j] == 1)
return false;
}
//check the left diagonal
for(int i=r,j=c; i>=0 && j>=0; i--,j--){
if(board[i][j] == 1)
return false;
}
//check the right diagonal
for(int i=r,j=c; i<n && j>=0; i++,j--){
if(board[i][j] == 1)
return false;
}
//return true because it is safe
return true;
}
}Output:
When N is 4:
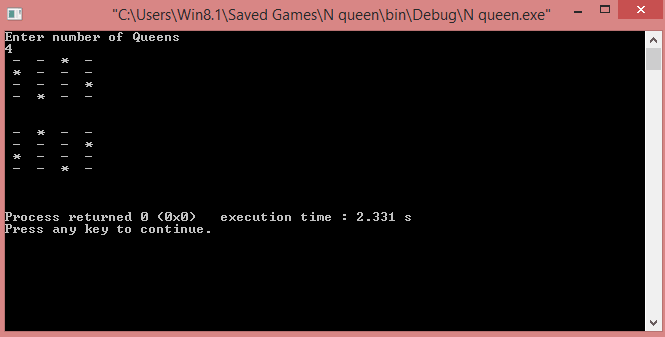
In the above program, the solveColumn(int col) is the recursive function implementing the backtracking algorithm.
The function checks whether it is possible or not to place a queen in a specific column. If yes it proceeds to the next recursive call i.e. solveColumn(col+1) else the execution returns back to the last recursive call to check for the next safe position..
There are 92 safe configurations possible for 8 queens in the 8×8 chessboard, so it is not possible to show output here.
Check the output yourself by giving the value of N during program execution.
In this tutorial, we learned what is N Queen Problem and how to solve the ‘N queen problem’ using backtracking algorithm in C and Java programming languages.
wow,so helpful
thank you so much for saving me.
one request sir
how to solve sum of subsets problem using backtracking.
please help 👨🦱
Check out I have posted the solution of Subset problem.