Problem: Given a maze in the form of a binary rectangular matrix, we have to find the shortest path from the given source to the given destination. The path can only be created with the cells of 1.
It is important to note that only vertical and horizontal movements are allowed.
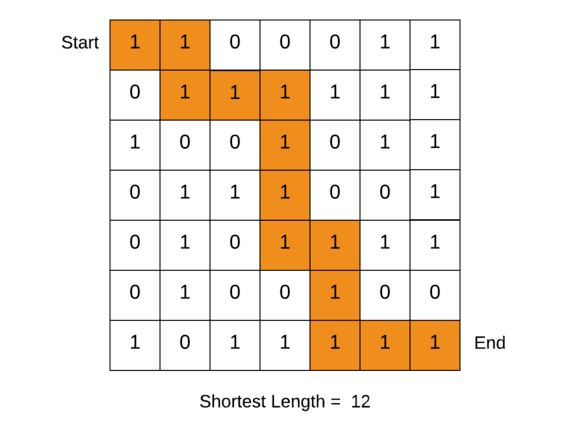
We can easily find the shortest path in the maze by using the backtracking algorithm.
The idea is to keep moving through a valid path until stuck, otherwise backtrack to the last traversed cell and explore other possible paths to the destination.
For each cell, the following 4 moves are possible:
- Up – (x, y-1)
- Down – (x, y+1)
- Right – (x+1, y)
- Left – (x-1, y)
We validate every move before undertaking it. If any move is not valid, we check for the next one.
For example, if the upper cell is zero, we test for the lower cell. If the lower cell also contains zero, we check for the right cell. If the right cell is also not valid, we go for the left cell if it is valid.
If non of the 4 moves are valid, we backtrack to the last visited cell to choose another cell (path) so that we can avoid the current cell which doesn’t have any path to the destination.
On reaching the destination, we deliberately backtrack to explore other possible paths to the destination cell.
After exhausting all possibilities, we output the path with the minimum length.
Here is the recursive implementation of the solution using backtracking in C++, Java and Python:
Python
import sys
#Maze in binary representation
matrix =[ [ 1, 1, 0, 0, 0, 1, 1],
[ 0, 1, 1, 1, 1, 1, 1],
[ 1, 0, 0, 1, 0, 1, 1],
[ 0, 1, 1, 1, 0, 0, 1],
[ 0, 1, 0, 1, 1, 1, 1],
[ 0, 1, 0, 0, 1, 0, 0],
[ 1, 0, 1, 1, 1, 1, 1] ]
#2D Array mapping to mark visited cell
visited = [[0 for x in range(len(matrix[0]))] for y in range(len(matrix))]
#Source and destination cell
start =(0,0)
end = (6,6)
#Initially storing the max possible integer as the shortest path length
shortLength = sys.maxsize
length=0
hasPath =False
#Function to initiate the search
def findPath():
visit(start[0], start[1])
#Function to visit a cell and recursively make next move
def visit(x, y):
global length, shortLength, visited, hasPath
#Base Condition - Reached the destination cell
if x==end[0]and y==end[1]:
#Update hasPath to True (Maze has a solution)
hasPath = True
#Store the minimum of the path length
shortLength = min(length, shortLength)
#Backtrack to explore more possible paths
return
#Mark current cell as visited
visited[x][y] = 1
#Increment the current path length by 1
length +=1
#Check for next move:
#1.Right
if canVisit(x+1, y):
visit(x+1, y)
#2.Down
if canVisit(x, y+1):
visit(x, y+1)
#3.Left
if canVisit(x-1, y):
visit(x-1, y)
#4.Up
if canVisit(x, y-1):
visit(x, y-1)
#Backtrack by unvisiting the current cell and
#decrementing the value of current path length
visited[x][y] = 0
length -= 1
#Function checks if (x,y) cell is valid cell or not
def canVisit(x, y):
#check maze boundaries
if x<0 or y<0 or x>=len(matrix[0]) or y>=len(matrix):
return False
#check 0 or already visited
if matrix[x][y]==0 or visited[x][y]==1:
return False
return True
#Driver code
if __name__ == '__main__':
findPath()
#output only if any path to the destination was found
if hasPath:
print(f"Shortest Path Length: {shortLength}")
else:
print("No Path Possible")
C++
#include <iostream>
#include <limits.h>
//Binary Representation of Maze
int matrix[7][7] =
{
{ 1, 1, 0, 0, 0, 1, 1},
{ 0, 1, 1, 1, 1, 1, 1},
{ 1, 0, 0, 1, 0, 1, 1},
{ 0, 1, 1, 1, 0, 0, 1},
{ 0, 1, 0, 1, 1, 1, 1},
{ 0, 1, 0, 0, 1, 0, 0},
{ 1, 0, 1, 1, 1, 1, 1}
};
//Maze Class
class Maze{
public:
int *start;
int *end;
int visited[7][7]= {0};
int shortLength=INT_MAX;
int length=0;
bool hasPath = false;
Maze(int start[], int end[]){
this->start = start;
this->end = end;
}
//Function to initiate search process
void findPath(){
visit(start[0], start[1]);
}
//Function to visit a cell and recursively make next move
void visit(int x, int y){
//Base Condition - Reached the destination cell
if(x==end[0] && y==end[1]){
//Update hasPath to True (Maze has a possible path)
hasPath=true;
//Store the minimum of the path length
if(length<shortLength)
shortLength=length;
//return (Backtrack) to explore more possible paths
return;
}
//Mark the current cell as visited
visited[x][y] = 1;
//Increment the current path length by 1
length++;
//Check for next move:
//1.Right
if(canVisit(x+1, y)){
visit(x+1, y);
}
//2.Down
if(canVisit(x, y+1)){
visit(x, y+1);
}
//3.Left
if(canVisit(x-1, y)){
visit(x-1, y);
}
//4.Up
if(canVisit(x, y-1)){
visit(x, y-1);
}
//Backtrack by unvisiting the current cell and
//decrementing the value of current path length
visited[x][y] = 0;
length--;
}
//Function checks if (x,y) is a vaid cell or not
bool canVisit(int x, int y){
//Number of Columns in Maze
int m=sizeof(matrix[0])/sizeof(matrix[0][0]);
//Number of rows in Maze
int n=sizeof(matrix)/sizeof(matrix[0]);
//Check Boundaries
if(x<0 || y<0 || x>=m || y>=n)
return false;
//Check 0 or already visited
if(matrix[x][y]==0 || visited[x][y]==1)
return false;
return true;
}
};
//Driver Code
int main() {
int start[] = {0, 0};
int end[] = {6, 6};
Maze maze(start, end);
maze.findPath();
//output if the maze has a solution
if(maze.hasPath)
std::cout << "Shortest Path Length: " << maze.shortLength;
else
std::cout << "No Path Possible";
}
Java
class Main {
public static void main(String[] args) {
//Matrix in Binary Format
int matrix[][] =
{
{ 1, 1, 0, 0, 0, 1, 1},
{ 0, 1, 1, 1, 1, 1, 1},
{ 1, 0, 0, 1, 0, 1, 1},
{ 0, 1, 1, 1, 0, 0, 1},
{ 0, 1, 0, 1, 1, 1, 1},
{ 0, 1, 0, 0, 1, 0, 0},
{ 1, 0, 1, 1, 1, 1, 1}
};
//Start and End cell
int start[] = {0, 0};
int end[] = {6, 6};
//Driver code
Maze maze = new Maze(matrix, start, end);
maze.findPath();
//Output the shortest length if the maze have any
if(maze.hasPath)
System.out.println("Shortest Path Length: "+maze.shortLength);
else
System.out.println("No Path Possible");
}
}
class Maze{
int matrix[][];
int visited[][];
int shortLength=Integer.MAX_VALUE;
int length=0;
boolean hasPath = false;
int start[];
int end[];
Maze(int matrix[][],int start[],int end[]){
this.matrix = matrix;
this.start =start;
this.end=end;
this.visited=new int[matrix.length][matrix.length];
}
//Function to initiate path search
public void findPath(){
visit(start[0], start[1]);
}
//Function to visit a cell and recursively move to next cell
private void visit(int x, int y){
//Base condition - Reached destination cell
if(x==end[0] && y==end[1]){
hasPath=true;
//Update lenght with the minimum length
if(length<shortLength)
shortLength=length;
//Return to explore more paths
return;
}
//Mark cell as visited
visited[x][y] = 1;
//Increment the length of the current path by 1
length++;
//Check and move to next cell:
//1.Right
if(canVisit(x+1, y)){
visit(x+1, y);
}
//2.Down
if(canVisit(x, y+1)){
visit(x, y+1);
}
//3.Left
if(canVisit(x-1, y)){
visit(x-1, y);
}
//4.Up
if(canVisit(x, y-1)){
visit(x, y-1);
}
//Backtrack - Unvisit the cell
visited[x][y] = 0;
//Decrement the current length path by 1
length--;
}
//Function check if (x,y) is a valid cell
private boolean canVisit(int x, int y){
//Check boundaries
if(x<0 || y<0 || x>=matrix[0].length || y>=matrix.length)
return false;
//Check for 0 and already visited cell
if(matrix[x][y]==0 || visited[x][y]==1)
return false;
return true;
}
} Output:
Shortest Path Length: 12In the above program, the visit(int x, int y) is the recursive function implementing the backtracking algorithm.
The canVisit(int x, int y) function checks whether the current cell is valid or not. We use this function to validate the moves.
We are using the visited[][] array to avoid cyclic traversing of the path by marking the cell as visited.
We visit a cell of the maze matrix by updating the corresponding cell in the visited[][] matrix with the value of 1 i.e. visited[x][y]=1.
Every time we mark a cell as visited we also increment the length of the current path. by 1 i.e. length++.
We recursively traverse the next valid cell until we reach the destination cell.
On reaching the destination cell we update the minimum path length i.e. shortLength = min(shortLength, length).
In the driver code of our program, we are initiating the search process and outputting the shortest path of the maze (if it has any).
The backtracking process of finding the shortest path in the maze is not efficient because it explores all possible paths to the destination, which may not be the final solution.
In this programming tutorial, we learned to find the shortest path in the binary maze using the backtracking algorithm in Python, C++, and Java Programming languages.
Nice explanation and I am also trying to solve a similar type of maze reading from a file. I also need to travel through 0s not 1s. But only right or left not diagonally. So My maze is as below : E is the entry and in any border if we hit any 0 i.e the exit. Currently only one exit at the last line. But there may be other exits too.
Input :
1E1111
101011
100001
110101
111101
Expected output :
Shortest path count and then
1E1111
1+1011
1++++1
1101+1
111101
I need to find shortest path and also I need to mark that short path with some symbols like + and also to print the maze at the end with those symbols updated ?
Any help on this would be appreciated ?
I could print steps count now with the algorithm. How to mark the path with +signs and then print maze at the end ?
Thank you!
Hey what will be the time complexity for this approach ? Is it O( 2^(M*N)) ? Please clarify. Thank you
Yes, the worst time complexity of this algorithm is O(2M*N).