Problem: Given an undirected graph, find and print all the Hamiltonian Cycles present in the graph.
What is the Hamiltonian cycle?
A Hamiltonian cycle also called a Hamiltonian circuit, is a graph cycle (i.e., closed-loop) through a graph that visits each node exactly once.
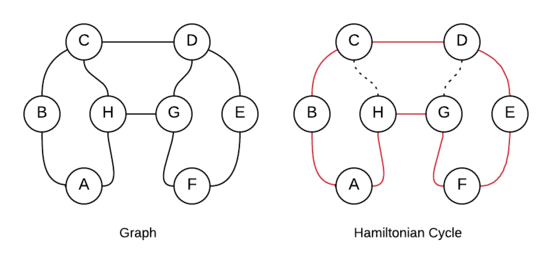
How to Find the Hamiltonian Cycle using Backtracking?
Using the backtracking method, we can easily find all the Hamiltonian Cycles present in the given graph.
The idea is to use the Depth-First Search algorithm to traverse the graph until all the vertices have been visited.
We traverse the graph starting from a vertex (arbitrary vertex chosen as starting vertex) and
At any point during the traversal we get stuck (i.e., all the neighbor vertices have been visited), we backtrack to find other paths (i.e., to visit another unvisited vertex).
If we successfully reach back to the starting vertex after visiting all the nodes, it means the graph has a Hamiltonian cycle otherwise not.
We mark each vertex as visited so that we don’t traverse them more than once.
Print All Hamiltonian Cycles present in the Graph (represented using Adjacency Matrix)
Adjacency Matrix is a 2D array that indicates whether the pair of nodes are adjacent or not in the graph.
Since adjacency matrix is an array, we will also represent the vertices as an array elements in our program.
Python
class Hamiltonian:
def __init__(self, start):
#start (& end) vertex
self.start = start
#list to store the cycle path
self.cycle = []
#varibale to mark if graph has the cycle
self.hasCycle = False
#method to inititate the search of cycle
def findCycle(self):
#add starting vertex to the list
self.cycle.append(self.start)
#start the search of the hamiltonian cycle
self.solve(self.start)
#recursive function to implement backtracking
def solve(self, vertex):
#Base condition: if the vertex is the start vertex
#and all nodes have been visited (start vertex twice)
if vertex == self.start and len(self.cycle) == N+1:
self.hasCycle = True
#output the cycle
self.displayCycle()
#return to explore more cycles
return
#iterate through the neighbor vertices
for i in range(len(vertices)):
if adjacencyM[vertex][i] == 1 and visited[i] == 0:
nbr = i
#visit and add vertex to the cycle
visited[nbr] = 1
self.cycle.append(nbr)
#traverse the neighbor vertex to find the cycle
self.solve(nbr)
#Backtrack
visited[nbr] = 0
self.cycle.pop()
#function to display the hamiltonian class
def displayCycle(self):
names = []
for v in self.cycle:
names.append(vertices[v])
print(names)
if __name__ == '__main__':
vertices = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
adjacencyM = [[0, 1, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 0, 0],
[0, 1, 0, 1, 0, 0, 0, 1],
[0, 0, 1, 0, 1, 0, 1, 0],
[0, 0, 0, 1, 0, 1, 0, 0],
[0, 0, 0, 0, 1, 0, 1, 0],
[0, 0, 0, 1, 0, 1, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0]]
#list mapping of vertices to mark vertex visited
visited = [0 for x in range(len(vertices))]
#number of vertices in the graph
N = 8
#Driver code
hamiltonian = Hamiltonian(0)
hamiltonian.findCycle()
#if the graph doesn't have any Hamiltonian Cycle
if not hamiltonian.hasCycle:
print("No Hamiltonian Cycle")
C++
#include <iostream>
#include <list>
using namespace std;
//number of vertices
#define N 8
//vertices
char vertices[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};
//adjacency matrix
int adjacencyM[N][N]= {{0, 1, 0, 0, 0, 0, 0, 1},
{1, 0, 1, 0, 0, 0, 0, 0},
{0, 1, 0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1, 0, 0},
{0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1, 0, 1},
{1, 0, 1, 0, 0, 0, 1, 0}};
//list mapping of vertices to mark vertex visited
int visited[N] {0};
class Hamiltonian{
public:
//start (& end) vertex
int start;
//stack used as list to store the path of the cycle
list<int> cycle;
//varibale to mark if graph has the cycle
bool hasCycle = false;
//constructor
Hamiltonian(int start){
this->start = start;
}
//method to inititate the search of the Hamiltonian cycle
void findCycle(){
//add starting vertex to the list
cycle.push_back(start);
//start searching the path
solve(start);
}
void solve(int vertex){
//Base condition: if the vertex is the start vertex
//and all nodes have been visited (start vertex twice)
if(vertex == start && cycle.size() == N+1){
hasCycle = true;
//output the cycle
displayCycle();
//return to explore more hamiltonian cycles
return;
}
//iterate through the neighbor vertices
for(int i=0; i<N; i++){
if(adjacencyM[vertex][i] == 1 && visited[i] == 0){
int nbr =i;
//visit and add vertex to the cycle
visited[nbr] = 1;
cycle.push_back(nbr);
//Go to the neighbor vertex to find the cycle
solve(nbr);
//Backtrack
visited[nbr] = 0;
cycle.pop_back();
}
}
}
//Function to display hamiltonian cycle
void displayCycle(){
cout << "[";
for(int v: cycle){
cout << vertices[v] << " " ;
}
cout << "] \n";
}
};
int main() {
//Driver code
Hamiltonian hamiltonian = Hamiltonian(0);
hamiltonian.findCycle();
//if the graph doesn't have any Hamiltonian Cycle
if(!hamiltonian.hasCycle){
cout << "No Hamiltonian Cycle";
}
}Java
import java.util.*;
class Hamiltonian{
//vertices
char vertices[];
//adjacency matrix
int adjacencyM[][];
//list mapping of vertices to mark vertex visited
int visited[];
//start (& end) vertex index
int start;
//stack used as list to store the path of the cycle
Stack<Integer> cycle = new Stack<>();
//number of vertices in the graph
int N;
//variable to mark if graph has the cycle
boolean hasCycle = false;
//constructor
Hamiltonian(int start, char vertices[], int adjacencyM[][]){
this.start = start;
this.vertices = vertices;
this.adjacencyM = adjacencyM;
this.N = vertices.length;
this.visited = new int[vertices.length];
}
//method to inititate the search of the Hamiltonian cycle
public void findCycle(){
//add starting vertex to the list
cycle.push(start);
//start searching the path
solve(start);
}
private void solve(int vertex){
//Base condition: if the vertex is the start vertex
//and all nodes have been visited (start vertex twice)
if(vertex == start && cycle.size() == N+1){
hasCycle = true;
//output the cycle
displayCycle();
//return to explore more hamiltonian cycles
return;
}
//iterate through the neighbor vertices
for(int i=0; i<N; i++){
if(adjacencyM[vertex][i] == 1 && visited[i] == 0){
int nbr =i;
//visit and add vertex to the cycle
visited[nbr] = 1;
cycle.push(nbr);
//Go to the neighbor vertex to find the cycle
solve(nbr);
//Backtrack
visited[nbr] = 0;
cycle.pop();
}
}
}
//Method to display the path of the cycle
void displayCycle(){
//converting vertex index to the name
List<Character> names = new ArrayList<>();
for(int idx: cycle){
names.add(vertices[idx]);
}
System.out.println(names);
}
}
class Main {
public static void main(String[] args) {
//vertices
char vertices[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};
//adjacency matrix
int adjacencyM[][]= {{0, 1, 0, 0, 0, 0, 0, 1},
{1, 0, 1, 0, 0, 0, 0, 0},
{0, 1, 0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1, 0, 0},
{0, 0, 0, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1, 0, 1},
{1, 0, 1, 0, 0, 0, 1, 0}};
//Driver code
Hamiltonian hamiltonian = new Hamiltonian(0,vertices, adjacencyM);
hamiltonian.findCycle();
//if the graph doesn't have any Hamiltonian Cycle
if(!hamiltonian.hasCycle){
System.out.println("No Hamiltonian Cycle");
}
}
}Output:
[A, B, C, D, E, F, G, H, A][A, H, G, F, E, D, C, B, A]
The solve() method of the Hamiltonian class is the recursive method implementing the backtracking algorithm.
As discussed, using DFS we traverse the graph, and every time we find a cycle (i.e., the base condition is satisfied), we output it and deliberately backtrack (i.e., return) to find more such cycles.
If the given graph does have any Hamiltonian cycle, the value of the hasCycle variable remains false. We use it in our main method to print output the respective result.
Print All Hamiltonian Cycles present in the Graph (represented using Adjacency List)
When a graph is represented using adjacency lists, every vertex holds a list that describes the set of its neighbor’s vertices.
In our program, we represent the vertex as a class with an adjacency list as it’s one of its properties and construct the graph by adding the connected vertices to their respective adjacency lists.
Python
#class representing vertex of a graph
class Vertex:
def __init__(self, name):
#name of the vertex e.g A or B
self.name = name
#boolen variable to mark vertex as visited
self.visited = False
#Adjacency List
self.neighbors = []
#method to connect two vertices
def add_neighbor(self, vertex):
self.neighbors.append(vertex)
vertex.neighbors.append(self)
#string representation of the Vertex
def __repr__(self):
return self.name
class Hamiltonian:
def __init__(self, start):
#start (& end) vertex
self.start = start
#list to store the cycle path
self.cycle = []
#varibale to mark if graph has the cycle
self.hasCycle = False
#method to inititate the search of cycle
def findCycle(self):
#add starting vertex to the list
self.cycle.append(self.start)
#start the search of the hamiltonian cycle
self.solve(self.start)
#recursive function to implement backtracking
def solve(self, vertex):
#Base condition: if the vertex is the start vertex
#and all nodes have been visited (start vertex twice)
if vertex == self.start and len(self.cycle) == N+1:
self.hasCycle = True
#output the cycle
print(self.cycle)
#return to explore more cycles
return
#iterate through the neighbor vertices
for nbr in vertex.neighbors:
#only if the neighbor vertex is not visited before
if not nbr.visited:
#visit and add vertex to the cycle
nbr.visited = True
self.cycle.append(nbr)
#Go to the neighbor vertex to find the cycle
self.solve(nbr)
#Backtrack
nbr.visited = False
self.cycle.pop()
if __name__ == '__main__':
#create vertices
vertex_A = Vertex('A')
vertex_B = Vertex('B')
vertex_C = Vertex('C')
vertex_D = Vertex('D')
vertex_E = Vertex('E')
vertex_F = Vertex('F')
vertex_G = Vertex('G')
vertex_H = Vertex('H')
#connect vertices i.e. create grpah
vertex_A.add_neighbor(vertex_B)
vertex_B.add_neighbor(vertex_C)
vertex_C.add_neighbor(vertex_D)
vertex_C.add_neighbor(vertex_H)
vertex_D.add_neighbor(vertex_E)
vertex_D.add_neighbor(vertex_G)
vertex_E.add_neighbor(vertex_F)
vertex_F.add_neighbor(vertex_G)
vertex_G.add_neighbor(vertex_H)
vertex_H.add_neighbor(vertex_A)
#number of vertices in the graph
N = 8
#Driver code
hamiltonian = Hamiltonian(vertex_A)
hamiltonian.findCycle()
#if the graph doesn't have any Hamiltonian Cycle
if not hamiltonian.hasCycle:
print("No Hamiltonian Cycle")
C++
#include <iostream>
#include <list>
using namespace std;
//class representing vertex of a graph
class Vertex{
public:
//name of the vertex
char name;
//variable to mark whether the vertex is visited or not
bool visited = false;
//Adjacency list
list<Vertex*> neighbors;
Vertex(char name){
this->name =name;
}
//method to connect two vertices
void add_neighbor(Vertex* vertex){
this->neighbors.push_front(vertex);
vertex->neighbors.push_front(this);
}
};
class Hamiltonian{
public:
//start (& end) vertex
Vertex* start;
//stack used as list to store the path of the cycle
list<Vertex*> cycle;
//number of vertices in the graph
int N;
//varibale to mark if graph has the cycle
bool hasCycle = false;
//constructor
Hamiltonian(Vertex* start, int N){
this->start = start;
this->N = N;
}
//method to inititate the search of the Hamiltonian cycle
void findCycle(){
//add starting vertex to the list
cycle.push_back(start);
//start searching the path
solve(start);
}
void solve(Vertex* vertex){
//Base condition: if the vertex is the start vertex
//and all nodes have been visited (start vertex twice)
if(vertex == start && cycle.size() == N+1){
hasCycle = true;
//output the cycle
displayCycle();
//return to explore more hamiltonian cycles
return;
}
//iterate through the neighbor vertices
for(Vertex* nbr: vertex->neighbors){
if(!nbr->visited){
//visit and add vertex to the cycle
nbr->visited = true;
cycle.push_back(nbr);
//Go to the neighbor vertex to find the cycle
solve(nbr);
//Backtrack
nbr->visited = false;
cycle.pop_back();
}
}
}
//Function to display hamiltonian cycle
void displayCycle(){
cout << "[";
for(Vertex* v: cycle){
cout << v->name << " " ;
}
cout << "] \n";
}
};
int main() {
//create vertices
Vertex* vertices[] ={
new Vertex('A'),
new Vertex('B'),
new Vertex('C'),
new Vertex('D'),
new Vertex('E'),
new Vertex('F'),
new Vertex('G'),
new Vertex('H')
};
//connect vertices i.e. create grpah
vertices[0]->add_neighbor(vertices[1]);
vertices[1]->add_neighbor(vertices[2]);
vertices[2]->add_neighbor(vertices[3]);
vertices[2]->add_neighbor(vertices[7]);
vertices[3]->add_neighbor(vertices[4]);
vertices[3]->add_neighbor(vertices[6]);
vertices[4]->add_neighbor(vertices[5]);
vertices[5]->add_neighbor(vertices[6]);
vertices[6]->add_neighbor(vertices[7]);
vertices[7]->add_neighbor(vertices[0]);
//Driver code
Hamiltonian hamiltonian = Hamiltonian(vertices[0], 8);
hamiltonian.findCycle();
//if the graph doesn't have any Hamiltonian Cycle
if(!hamiltonian.hasCycle){
cout << "No Hamiltonian Cycle";
}
}Java
import java.util.*;
//class representing vertex of a graph
class Vertex{
//name of the vertex
Character name;
//variable to mark whether the vertex is visited or not
boolean visited = false;
//Adjacency list
List<Vertex> neighbors = new ArrayList<>();
Vertex(char name){
this.name = name;
}
//method to connect two vertices
public void add_neighbor(Vertex vertex){
this.neighbors.add(vertex);
vertex.neighbors.add(this);
}
//String representation of the class
public String toString(){
return name.toString();
}
}
class Hamiltonian{
//start (& end) vertex
Vertex start;
//stack used as list to store the path of the cycle
Stack<Vertex> cycle = new Stack<>();
//number of vertices in the graph
int N;
//varibale to mark if graph has the cycle
boolean hasCycle = false;
//constructor
Hamiltonian(Vertex start, int N){
this.start = start;
this.N = N;
}
//method to inititate the search of the Hamiltonian cycle
public void findCycle(){
//add starting vertex to the list
cycle.push(start);
//start searching the path
solve(start);
}
private void solve(Vertex vertex){
//Base condition: if the vertex is the start vertex
//and all nodes have been visited (start vertex twice)
if(vertex == start && cycle.size() == N+1){
hasCycle = true;
//output the cycle
System.out.println(cycle);
//return to explore more hamiltonian cycles
return;
}
//iterate through the neighbor vertices
for(Vertex nbr: vertex.neighbors){
if(!nbr.visited){
//visit and add vertex to the cycle
nbr.visited = true;
cycle.push(nbr);
//Go to the neighbor vertex to find the cycle
solve(nbr);
//Backtrack
nbr.visited = false;
cycle.pop();
}
}
}
}
class Main {
public static void main(String[] args) {
//create vertices
Vertex vertices[] ={
new Vertex('A'),
new Vertex('B'),
new Vertex('C'),
new Vertex('D'),
new Vertex('E'),
new Vertex('F'),
new Vertex('G'),
new Vertex('H')
};
//connect vertices i.e. create grpah
vertices[0].add_neighbor(vertices[1]);
vertices[1].add_neighbor(vertices[2]);
vertices[2].add_neighbor(vertices[3]);
vertices[2].add_neighbor(vertices[7]);
vertices[3].add_neighbor(vertices[4]);
vertices[3].add_neighbor(vertices[6]);
vertices[4].add_neighbor(vertices[5]);
vertices[5].add_neighbor(vertices[6]);
vertices[6].add_neighbor(vertices[7]);
vertices[7].add_neighbor(vertices[0]);
//Driver code
Hamiltonian hamiltonian = new Hamiltonian(vertices[0], vertices.length);
hamiltonian.findCycle();
//if the graph doesn't have any Hamiltonian Cycle
if(!hamiltonian.hasCycle){
System.out.println("No Hamiltonian Cycle");
}
}
}Output:
[A, B, C, D, E, F, G, H, A][A, H, G, F, E, D, C, B, A]
The output contains the paths of the Hamiltonian cycles present in the given undirected graph.
In this tutorial, we learned what Hamiltonian Cycle is and how to find and print all Hamiltonian cycles present in an undirected graph using the backtracking algorithm.