Summary: In this post, we will learn what the Subset Sum Problem is and how to solve the Subset Sum Problem using the backtracking algorithm in C++ and Java.
What is Subset Sum Problem?
Given a set of elements and a sum value. We need to find all possible subsets of the elements with a sum equal to the sum value.
Example:
- Set: {10, 7, 5, 18, 12, 20, 15}
- Sum: 30
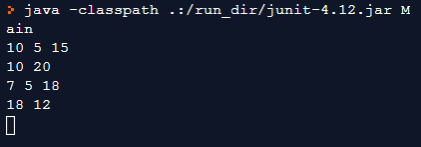
- Output: [ {10, 5, 15}, {10, 20}, {7, 5, 18}, {18, 12} ]
There are two ways to solve the Subset Sum Problem:
- Brute Force – Slow
- Backtracking – Fast
In the Bruteforce approach, we usually test every combination starting from one, then two, then three, and so on for the required sum.
Using Backtracking we can reduce its time complexity up to a great extent. Let’s see how.
Subset Sum Problem Solution using Backtracking Algorithm
The main idea is to add the number to the stack and track the sum of stack values.
Add a number to the stack, and check if the sum of all elements is equal to the sum. If yes then print the stack, else if the stack elements are less than the sum then repeat the step by adding the next element to the stack.
If the sum of stack elements exceeds the sum value then pop the last inserted element (top value) and repeat the process by adding the next available element.
In order to pop an element we need to backtrack, therefore we will use recursion.
The solution for the subset-sum is similar to the solution of N Queen Problem using Backtracking.
Recommeded: What is Backtracking Algorithm?
Let’s see the algorithm to solve sum of subset problems in code.
Java
import java.util.Stack;
class SubSet{
int set[];
int sum;
Stack<Integer> solutionSet;
boolean hasSolution;
SubSet(int set[], int sum){
this.set = set;
this.sum = sum;
this.solutionSet = new Stack<>();
hasSolution = false;
}
public void solve(int s, int idx){
//return false if s value exceed sum
if(s>sum)
return;
//check if stack has the right subsets of numbers
if(s==sum){
hasSolution = true;
//display stack contents
displaySolutionSet();
//Though found a solution but deliberately returning to find more
return;
}
for(int i=idx; i<set.length; i++){
//Adding element to the stack
solutionSet.push(set[i]);
//add set[i] to the 's' and recusively start from next number
solve(s+set[i],i+1);
//Removing element from stack i.e Backtracking
solutionSet.pop();
}
}
//Function to display stack content
private void displaySolutionSet(){
for (Integer item: solutionSet){
System.out.print(item+" ");
}
System.out.println();
}
}
public class Main
{
public static void main(String[] args) {
int set[] = {10, 7, 5, 18, 12, 20, 15};
int size = 30;
SubSet ss = new SubSet(set, size);
ss.solve(0,0);
if(ss.hasSolution == false)
System.out.print("No Solution");
}
}C++
#include <iostream>
#include <stack>
using namespace std;
int set[] = {10, 7, 5, 18, 12, 20, 15};
int numberOfElements = 7, sum = 30;
class SubSet{
public:
stack<int> solutionSet;
bool hasSolution;
void solve(int s, int idx){
//return if s exceed sum
if(s>sum)
return;
//check if stack has the right subsets of numbers
if(s==sum){
hasSolution = true;
//display stack contents
displaySolutionSet();
//Though found a solution but deliberately
//returning to find more
return;
}
for(int i=idx; i<numberOfElements; i++){
//Adding element to the stack
solutionSet.push(set[i]);
//add set[i] to the 's' and recusively start from next number
solve(s+set[i],i+1);
//Removing element from stack i.e Backtracking
solutionSet.pop();
}
}
//Function to display stack content
void displaySolutionSet(){
stack<int> temp;
while (!solutionSet.empty())
{
cout << solutionSet.top() << " ";
temp.push(solutionSet.top());
solutionSet.pop();
}
cout << '\n';
while (!temp.empty())
{
solutionSet.push(temp.top());
temp.pop();
}
}
};
int main()
{
SubSet ss;
ss.solve(0,0);
if(ss.hasSolution == false)
cout << "No Solution";
return 0;
}Output:
In the program, we add the set element to s by recursively passing the s+set[i] argument to the solve(int s, int idx) method.
Whenever the sum of stack elements equals the sum i.e. s==sum, we output the stack elements and deliberately return to look for more possible solutions.
If the stack sum exceeds sum i.e. s>sum, we return to the last recursive call to backtrack (i.e. to pop an element from the stack and push another element if available).
The displaySolutionSet() display stack elements whenever a solution has been found.
If there is no solution the value of the hasSolution remains false otherwise we update it to true.
In this tutorial, we learned what is subset sum problem and the solution for the subset sum problem using backtracking in C++ and Java programming languages.