Summary: In this post, we will learn What Sudoku is and how to solve the sudoku puzzle using the backtracking algorithm in C, C++, and Java.
What is Sudoku?
Sudoku is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 subgrids that compose the grid contain all of the digits from 1 to 9.
Initially, we are given a partially-filled grid like the following:

We need to fill the blanks cells such that the same number should not appear twice in the corresponding row + column and in any of the nine 3×3 subregions/boxes of the grid.

Sudoku Solution using Backtracking Algorithm
We can easily solve sudoku using the backtracking approach as follows:
- We will fill the cells column vise.
- For every cell, we will check if it is empty (or has 0) or not.
- If the cell is empty, we will then check which number from 1 to 9 is valid for the particular cell and update the cell accordingly.
- If the current cell is not empty, we will move to the next cell of the same column or first row of the next column if at the last cell of the column.
- If none of the numbers from 1 to 9 is valid for the current cell, we will go back to the last updated cell and try with another valid value (i.e. backtrack).
- To achieve backtracking, we will return to the last recursive call by returning
falsecheck with the next value of the iteration of ‘for loop’. We again proceed to the next cell after updating the last cell with another valid value.
To implement backtracking, we will use recursion with the following base condition:
//if reached the 10th column (passed 9th)
//sudoku filling completed, so display board
if(col == 9){
displayBoard();
return true;
}Here is the full implementation of the above discussed algorithm in Java and C++.
Java
class Sudoko{
int board[][];
Sudoko(int board[][]){
this.board = board;
}
public boolean solve(int row, int col){
//if reached the 10th column (passed 9th)
//sudoku filling completed, so display board
if(col == 9){
displayBoard();
return true;
}
//If cell already has a number
if(board[row][col] != 0){
if(row == 8) return solve(0,col+1);
else return solve(row+1,col);
}
//If cell is blank
for(int i=1; i<=9; i++){
//Place a number in the cell
board[row][col] = i;
//check if the placed number is valid
if(isValid(row,col)){
//Yes
//If reached at last row then move to
//starting of next column
if(row == 8){
if(solve(0,col+1))
return true;
}
else{
//Next cell of the same column
if(solve(row+1,col))
return true;
}
}
}
//Reset and Backtrack
board[row][col] = 0;
return false;
}
//Function to display board
private void displayBoard(){
for(int i=0; i<9; i++){
for(int j=0; j<9; j++){
System.out.print(board[i][j]+" ");
}
System.out.println();
}
System.out.println("\n\n");
}
//Function to check if the current placement in
//board[row][column] is valid or not
private boolean isValid(int row, int column){
//Checking he column (horizontal)
for(int i=0; i<9; i++){
if((board[row][i] == board[row][column]) && (i != column))
return false;
}
//Checking the row (vertical)
for(int i=0; i<9; i++){
if((board[i][column] == board[row][column]) && (i != row))
return false;
}
//Computing starting point of the current Grid
int sr = (row/3)*3;
int sc = (column/3)*3;
//Checking the grid (3x3)
for(int i=sr; i<sr+3; i++){
for(int j=sc; j<sc+3; j++){
if(board[row][column] == board[i][j] && (row != i) && (column != j))
return false;
}
}
return true;
}
}
public class Main
{
public static void main(String[] args) {
int board[][] = {{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}};
Sudoko sudoko = new Sudoko(board);
sudoko.solve(0,0);
}
}C++
#include <iostream>
using namespace std;
int board[9][9] = {{5, 3, 0, 0, 7, 0, 0, 0, 0},
{6, 0, 0, 1, 9, 5, 0, 0, 0},
{0, 9, 8, 0, 0, 0, 0, 6, 0},
{8, 0, 0, 0, 6, 0, 0, 0, 3},
{4, 0, 0, 8, 0, 3, 0, 0, 1},
{7, 0, 0, 0, 2, 0, 0, 0, 6},
{0, 6, 0, 0, 0, 0, 2, 8, 0},
{0, 0, 0, 4, 1, 9, 0, 0, 5},
{0, 0, 0, 0, 8, 0, 0, 7, 9}};
class Sudoko{
public:
bool solve(int row, int col){
//if reached the 10th column (passed 9th)
//sudoku filling completed, so display board
if(col == 9){
displayBoard();
return true;
}
//If cell already has a number
if(board[row][col] != 0){
if(row == 8) return solve(0,col+1);
else return solve(row+1,col);
}
//If cell is blank
for(int i=1; i<=9; i++){
//Place a number in the cell
board[row][col] = i;
//check if the placed number is valid
if(isValid(row,col)){
//Yes
//If reached at last row then move to
//starting of next column
if(row == 8){
if(solve(0,col+1))
return true;
}
else{
//Next cell of the same column
if(solve(row+1,col))
return true;
}
}
}
//Reset and Backtrack
board[row][col] = 0;
return false;
}
//Function to display board
void displayBoard(){
for(int i=0; i<9; i++){
for(int j=0; j<9; j++){
cout << board[i][j] << " ";
}
cout << "\n";
}
cout << "\n\n";
}
//Function to check if the current placement in
//board[row][column] is valid or not
bool isValid(int row, int column){
//Checking he column (horizontal)
for(int i=0; i<9; i++){
if((board[row][i] == board[row][column]) && (i != column))
return false;
}
//Checking the row (vertical)
for(int i=0; i<9; i++){
if((board[i][column] == board[row][column]) && (i != row))
return false;
}
//Computing starting point of the current Grid
int sr = (row/3)*3;
int sc = (column/3)*3;
//Checking the grid (3x3)
for(int i=sr; i<sr+3; i++){
for(int j=sc; j<sc+3; j++){
if(board[row][column] == board[i][j] && (row != i) && (column != j))
return false;
}
}
return true;
}
};
int main()
{
Sudoko sudoko;
sudoko.solve(0,0);
return 0;
}Output:
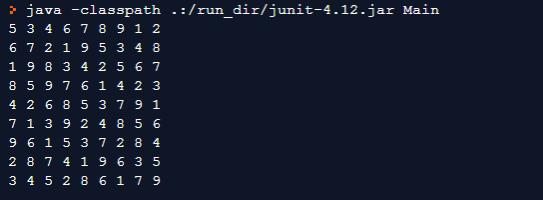
In this tutorial, we learned to solve Sudoku Puzzle programmatically using the backtracking algorithm in C++ and Java programming languages.