What is Graph Coloring Problem?
We have been given a graph and we are asked to color all vertices with the ‘M’ number of given colors, in such a way that no two adjacent vertices should have the same color.
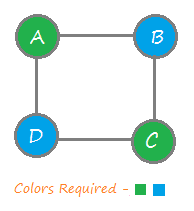
It it is possible to color all the vertices with the given colors then we have to output the colored result, otherwise output ‘no solution possible’.
The least possible value of ‘m’ required to color the graph successfully is known as the chromatic number of the given graph.
Graph Coloring Solution
Using Naive Algorithm
In this approach using the brute force method, we find all permutations of color combinations that can color the graph.
If any of the permutations is valid for the given graph and colors, we output the result otherwise not.
This method is not efficient in terms of time complexity because it finds all colors combinations rather than a single solution.
Using Backtracking Algorithm
The backtracking algorithm makes the process efficient by avoiding many bad decisions made in naïve approaches.
In this approach, we color a single vertex and then move to its adjacent (connected) vertex to color it with different color.
After coloring, we again move to another adjacent vertex that is uncolored and repeat the process until all vertices of the given graph are colored.
In case, we find a vertex that has all adjacent vertices colored and no color is left to make it color different, we backtrack and change the color of the last colored vertices and again proceed further.
If by backtracking, we come back to the same vertex from where we started and all colors were tried on it, then it means the given number of colors (i.e. ‘m’) is insufficient to color the given graph and we require more colors (i.e. a bigger chromatic number).
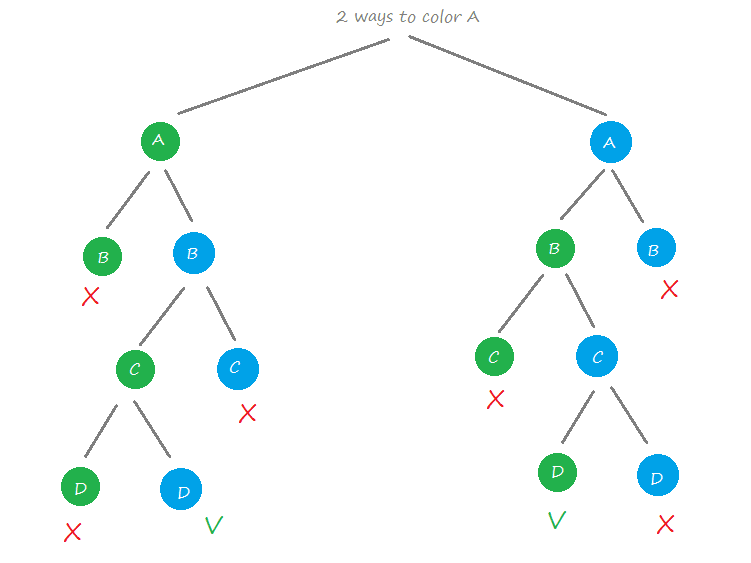
Steps To color graph using the Backtracking Algorithm:
- Different colors:
- Confirm whether it is valid to color the current vertex with the current color (by checking whether any of its adjacent vertices are colored with the same color).
- If yes then color it and otherwise try a different color.
- Check if all vertices are colored or not.
- If not then move to the next adjacent uncolored vertex.
- If no other color is available then backtrack (i.e. un-color last colored vertex).
Here backtracking means to stop further recursive calls on adjacent vertices by returning false. In this algorithm Step-1.2 (Continue) and Step-2 (backtracking) is causing the program to try different color option.
Continue – try a different color for current vertex.
Backtrack – try a different color for last colored vertex.
Here is the solution to the graph coloring problem in C and Java using the backtracking algorithm:
C
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
//Number of vertices
#define numOfVertices 4
// 0 - Green, 1 - Blue
char colors[][30] = {"Green", "Blue"};
int color_used = 2;
int colorCount;
//Graph connections
int graph[numOfVertices][numOfVertices] = {{0, 1, 0, 1},
{1, 0, 1, 0},
{0, 1, 0, 1},
{1, 0, 1, 0}};
//Vertex
typedef struct{
char name;
bool colored;
int color;
} Vertex;
//VertexList
Vertex *vertexArray[numOfVertices];
//function check if a vertex has any uncolored neighbors
int hasUncoloredNeighbours(int idx){
for(int i=0;i<numOfVertices; i++){
if(graph[idx][i] == 1 && vertexArray[i]->colored == false)
return i;
}
return -1;
}
//Function to check whether it is valid to color with color[colorIndex]
bool canColorWith(int colorIndex, int vertex) {
Vertex *neighborVertex;
for(int i=0; i<numOfVertices; i++){
//skipping if vertex are not connected
if(graph[vertex][i] == 0) continue;
neighborVertex = vertexArray[i];
if(neighborVertex->colored && neighborVertex->color == colorIndex)
return false;
}
return true;
}
//function to color the vertex
bool setColors(int idx){
int colorIndex, unColoredIdx;
//Step: 1
for (colorIndex=0; colorIndex<color_used; colorIndex++){
// Step-1.1 : checking validity
if(!canColorWith(colorIndex, idx)) continue;
//Step-1.2 : coloring
vertexArray[idx]->color = colorIndex;
vertexArray[idx]->colored = true;
colorCount++;
//Step-1.3 : Whether all vertices colored?
if(colorCount == numOfVertices ) //Base Case
return true;
//Step-1.4 : Next uncolored vertex
while((unColoredIdx = hasUncoloredNeighbours(idx)) != -1){
if(setColors(unColoredIdx))
return true;
}
}
// Step-2 : Backtracking
vertexArray[idx]->color = -1;
vertexArray[idx]->colored = false;
return false;
}
int main()
{
//define Vertex
Vertex vertexA, vertexB, vertexC, vertexD;
vertexA.name = 'A';
vertexB.name = 'B';
vertexC.name = 'C';
vertexD.name = 'D';
//add veritces to the array
vertexArray[0] = &vertexA;
vertexArray[1] = &vertexB;
vertexArray[2] = &vertexC;
vertexArray[3] = &vertexD;
//set default values (uncolor) for all vertices
for(int i=0; i<numOfVertices;i++){
vertexArray[i]->colored = false;
vertexArray[i]->color = -1;
}
//start coloring with first vertex
bool hasSolution = setColors(0);
//check if all vertices was successfully colored
if (!hasSolution)
printf("No Solution");
else {
for(int i=0; i<numOfVertices;i++){
printf("%c %s \n",vertexArray[i]->name,colors[vertexArray[i]->color]);
}
}
return 0;
}
Java
import java.util.ArrayList;
import java.util.List;
class Vertex {
String name;
List<Vertex> adjacentVertices;
boolean colored;
String color;
public Vertex(String name) {
this.name = name;
this.adjacentVertices = new ArrayList<>();
this.colored =false;
this.color = "";
}
//connect two verticess bi-directional
public void addNeighbor(Vertex vertex){
this.adjacentVertices.add(vertex);
vertex.adjacentVertices.add(this);
}
}
class Coloring {
String colors[];
int colorCount;
int numberOfVertices;
public Coloring(String[] colors, int N) {
this.colors = colors;
this.numberOfVertices = N;
}
public boolean setColors(Vertex vertex){
//Step: 1
for(int colorIndex=0; colorIndex<colors.length; colorIndex++){
//Step-1.1: checking validity
if(!canColorWith(colorIndex, vertex))
continue;
//Step-1.2: continue coloring
vertex.color=colors[colorIndex];
vertex.colored=true;
colorCount++;
//Step-1.3: check whether all vertices colored?
if(colorCount== numberOfVertices) //base case
return true;
//Step-1.4: next uncolored vertex
for(Vertex nbrvertex: vertex.adjacentVertices){
if (!nbrvertex.colored){
if(setColors(nbrvertex))
return true;
}
}
}
//Step-4: backtrack
vertex.colored = false;
vertex.color = "";
return false;
}
//Function to check whether it is valid to color with color[colorIndex]
boolean canColorWith(int colorIndex, Vertex vertex) {
for(Vertex nbrvertex: vertex.adjacentVertices){
if(nbrvertex.colored && nbrvertex.color.equals(colors[colorIndex]))
return false;
}
return true;
}
}
public class Main{
public static void main(String args[]){
//define vertices
Vertex vertices[]= {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D")};
//join verices
vertices[0].addNeighbor(vertices[1]);
vertices[1].addNeighbor(vertices[2]);
vertices[2].addNeighbor(vertices[3]);
vertices[0].addNeighbor(vertices[3]);
//define colors
String colors[] = {"Green","Blue"};
//create coloring object
Coloring coloring = new Coloring(colors, vertices.length);
//start coloring with vertex-A
boolean hasSolution = coloring.setColors(vertices[0]);
//check if coloring was successful
if (!hasSolution)
System.out.println("No Solution");
else {
for (Vertex vertex: vertices){
System.out.println(vertex.name + " "+ vertex.color +"\n");
}
}
}
}
Output:
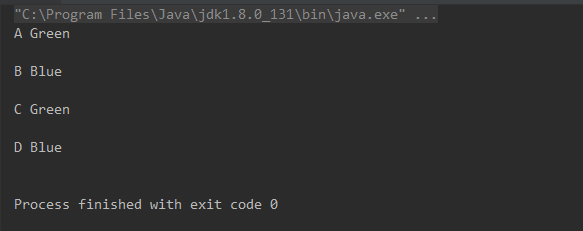
Note: Tb backtrack, we are returning false. By doing so the program comes back to the last recursive call to change the color of the last colored vertex. If false is returned by the starting vertex then it means there is no solution.
In the above program, we have created the same graph as depicted in the first picture and successfully colored the graph using the backtracking algorithm.
Hello,
I am learning the graph algorithm and I liked your program very much.
I have GitHub Repository that contains my learning and study on the topic.
Can I have include your program on my GitHub Repository with the link as the reference and the author within my program?
Ok
Thing does not work when you add more vertices
After adding new vertices to the array, make sure you also join them using the addNeighbor() method.