Problem: Given an unweighted undirected graph, we have to find the shortest path from the given source to the given destination using the Breadth-First Search algorithm.
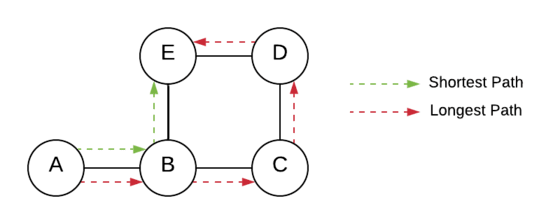
The idea is to traverse the graph using Breadth-First Search Traversal until we reach the end node and print the route by tracing back the path to the start node.
How to check whether recached the end node?
Every time we visit a node, we compare it with the end node. If they match, we stop BFS.
How to stop BFS when we reach the end node?
BFS uses the queue to visit the next node, it runs until the queue is empty.
So, we can either clear the queue to stop BFS or use an explicit boolean flag such as end_reached to mark the end of BFS.
How to trace path from end to start node?
To trace the route, we use an extra node property called prev that stores the reference of the preceding node.
Every time we visit a node, we also update its prev value.
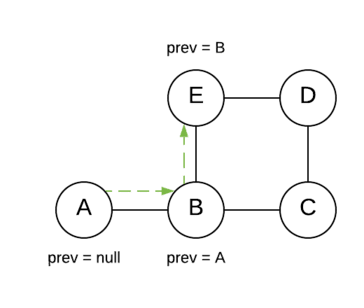
Using the prev value, we trace the route back from the end node to the starting node. Example for the given graph, route = E <- B <- A
Shortest Path in Unweighted Graph (represented using Adjacency List) using BFS
Every vertex (or node) in the graph has an adjacency list that describes the set of its neighbors.
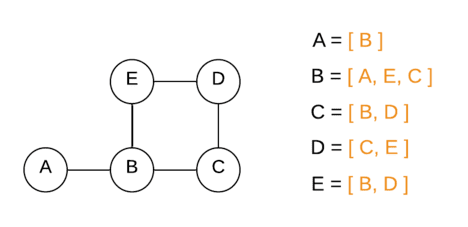
In our program, we represent every node as a class object with the following attributes:
neighbors– Adjacency list to store neighbor nodes.name– Name of the node.visited– To mark the node has been visited.prev– For storing the reference to the preceding node.
Here is the implementation of the algorithm for the above given unweighted graph in C++, Java and Python:
Python
#class representing node of a graph
class Node:
def __init__(self, name):
self.name = name
self.prev = None
self.neighbors = []
self.visited = False
#Method to connect nodes
def add_neighbor(self, node):
self.neighbors.append(node)
node.neighbors.append(self)
#Node representaion
def __repr__(self):
return self.name
class ShortestPath:
def __init__(self, start, end):
self.start = start
self.end = end
def bfs(self):
#Create queue
queue = []
#Visit and add the start node to the queue
self.start.visited = True
queue.append(self.start)
#BFS until queue is empty
while queue:
#Pop a node from queue for search operation
current_node = queue.pop(0)
#Loop through neighbors nodes to find the 'end' node
for node in current_node.neighbors:
if not node.visited:
#visit and add neighbors nodes to the queue
node.visited = True
queue.append(node)
#update its preceding node
node.prev = current_node
#stop BFS if the visited node is the end node
if node == self.end:
queue.clear()
break;
#BFS completed, now trace the route
self.trace_route()
#Function to trace the route using preceding nodes
def trace_route(self):
node = self.end
route = []
#start node has no preceding node
#so loop until node->prev is null
while node:
route.append(node)
node = node.prev
#reverse the route bring start to the front
route.reverse()
#output route
print(route)
if __name__ == '__main__':
#create nodes
node_A = Node('A')
node_B = Node('B')
node_C = Node('C')
node_D = Node('D')
node_E = Node('E')
#connect nodes (i.e. create graph)
node_A.add_neighbor(node_B)
node_B.add_neighbor(node_C)
node_C.add_neighbor(node_D)
node_D.add_neighbor(node_E)
node_B.add_neighbor(node_E)
ShortestPath(node_A, node_E).bfs()C++
#include <iostream>
#include <queue>
#include<list>
using namespace std;
//class representing node of a graph
class Node{
public:
//Adjacency List of the vertex
list<Node*> neighbors;
char name;
bool visited = false;
Node* prev = nullptr;
Node(char name){ this->name = name;}
//Method to connect vertices
void addNeighbour(Node* v){
this->neighbors.push_back(v);
v->neighbors.push_back(this);
}
};
class BFS{
Node* start;
Node* end;
public:
BFS(Node* start, Node* end){
this->start = start;
this->end = end;
}
void findPath(){
//Create queue and declare variables
queue<Node*> Queue;
bool reached_end = false;
//Visit start node and add to queue
start->visited = true;
Queue.push(start);
//BFS until queue is empty
while(!Queue.empty() && !reached_end){
//Pop a node from queue for search operation
Node* current_node=Queue.front();
Queue.pop();
//Loop through neighbors nodes to find the 'end' node
for(Node* node: current_node->neighbors){
if(!node->visited){
//Visit and add neighbor nodes to the queue
node->visited= true;
Queue.push(node);
node->prev = current_node;
//stop BFS if the end node is found
if(node == end){
reached_end = true;
break;
}
}
}
}
trace_route();
}
//Function to trace back route
void trace_route(){
list<Node*> route;
Node* node = end;
//start.prev is always null
//so loop until node->prev is null to trace route
while(node != nullptr){
route.push_front(node);
node = node->prev;
}
//Display the route
for(Node* n: route){
cout << n->name <<" ";
}
}
};
int main()
{
//create nodes
Node node_A('A'), node_B('B'), node_C('C'), node_D('D'), node_E('E');
//connect nodes (i.e. create graph)
node_A.addNeighbour(&node_B);
node_B.addNeighbour(&node_C);
node_C.addNeighbour(&node_C);
node_D.addNeighbour(&node_D);
node_B.addNeighbour(&node_E);
//Driver Code
BFS bfs(&node_A, &node_E);
bfs.findPath();
}Java
import java.util.*;
//Class representing graph nodes
class Node{
String name;
List<Node> neighbors;
boolean visited = false;
Node prev = null;
Node(String name){
this.name = name;
this.neighbors = new ArrayList<>();
}
//Method to connect nodes
void add_neighbor(Node node){
this.neighbors.add(node);
node.neighbors.add(this);
}
//Node representation
public String toString(){
return this.name;
}
}
//class implmenting the algorithm
class ShortestPath{
Node start, end;
ShortestPath(Node start, Node end){
this.start = start;
this.end = end;
}
public void bfs(){
//Create queue
Queue<Node> queue = new LinkedList<>();
//Visit and add start node to the queue
start.visited = true;
queue.add(start);
//BFS until queue is empty and not reached to the end node
while(!queue.isEmpty()){
//pop a node from queue for search operation
Node current_node = queue.poll();
//Loop through neighbors node to find the 'end'
for(Node node: current_node.neighbors){
if(!node.visited){
//Visit and add the node to the queue
node.visited =true;
queue.add(node);
//update its precedings nodes
node.prev = current_node;
//If reached the end node then stop BFS
if(node==end){
queue.clear();
break;
}
}
}
}
trace_route();
}
//Function to trace the route using preceding nodes
private void trace_route(){
Node node = end;
List<Node> route = new ArrayList<>();
//Loop until node is null to reach start node
//becasue start.prev == null
while(node != null){
route.add(node);
node = node.prev;
}
//Reverse the route - bring start to the front
Collections.reverse(route);
//Output the route
System.out.println(route);
}
}
//Driver Code
class Main {
public static void main(String[] args) {
//create nodes
Node node_A = new Node("A");
Node node_B = new Node("B");
Node node_C = new Node("C");
Node node_D = new Node("D");
Node node_E = new Node("E");
//connect nodes (i.e. create graph)
node_A.add_neighbor(node_B);
node_B.add_neighbor(node_C);
node_C.add_neighbor(node_D);
node_D.add_neighbor(node_E);
node_B.add_neighbor(node_E);
new ShortestPath(node_A, node_E).bfs();
}
}Output:
[A, B, E]Since we are generating the route from end node to the start node, we have to reverse the route list to correct its order.
Shortest Path in Unweighted Graph (represented using Adjacency Matrix) using BFS
Adjacency Matrix is an 2D array that indicates whether the pair of nodes are adjacent or not in the graph.
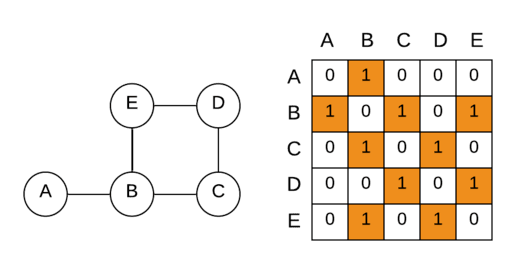
Since we are representing the graph using an adjacency matrix, it will be best to also mark visited nodes and store preceding nodes using arrays.
Here are the implementations of the algorithm for the above given unweighted graph using BFS in Python, C++ and Java:
Python
class ShortestPath:
def __init__(self, start, end):
self.start = start
self.end = end
def bfs(self):
queue = []
#Visit and add the start node to the queue
visited[self.start] = 1
queue.append(self.start)
#BFS until queue is empty
while queue:
#Pop a node from queue for search operation
current_node = queue.pop(0)
#Loop through neighbors nodes to find the 'end' node
#add unvisited neighbors to the queue
while self.unvisitedNeighbor(current_node) != -1:
neighbor_node = self.unvisitedNeighbor(current_node)
#Visit and add neighbor nodes to the queue
visited[neighbor_node] = 1;
queue.append(neighbor_node);
#update preceding node
prev[neighbor_node] = current_node;
#stop BFS if the end node is found
if neighbor_node == self.end:
queue.clear()
break
#BFS completed, now trace the route
self.trace_route()
#Function returns the index of unvisited neighbors
def unvisitedNeighbor(self, index):
for i in range(len(nodes_names)):
if adjacencyM[index][i] == 1 and visited[i] == 0:
return i
return -1
#Function to trace the route using preceding nodes
def trace_route(self):
node = self.end
route = []
#start node has no preceding node
#so loop until node->prev is null
while node != -1:
route.append(nodes_names[node])
node = prev[node]
#reverse the route bring start to the front
route.reverse()
#output route
print(route)
if __name__ == '__main__':
#vertices or nodes
nodes_names = ['A', 'B', 'C', 'D', 'E'];
#Adjacency Matrix
adjacencyM = [[0, 1, 0, 0, 0],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 1],
[0, 0, 1 ,0, 1],
[0, 1, 0, 1, 0]];
#List to mark visited nodes
visited = [0 for x in range(len(nodes_names))]
#List to stores preceding nodes
prev = [-1 for x in range(len(nodes_names))]
#Driver code
sp = ShortestPath(0, 4)
sp.bfs()C++
#include <iostream>
#include <queue>
#include<list>
#define N 6
using namespace std;
//vertices or nodes
char nodes_name[] = {'A', 'B', 'C', 'D', 'E'};
//Adjacency Matrix
int adjacencyM[N][N] = {{0, 1, 0, 0, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 1},
{0, 0, 1 ,0, 1},
{0, 1, 0, 1, 0}};
class ShortestPath{
//array to store preceding nodes
int prev[N] = {-1};
//array mapping to make visited vertices
int visited[N] = {0};
//start and end nodes index
int start, end;
public:
ShortestPath(int start, int end){
this->start = start;
this->end = end;
}
void bfs(){
//Create queue
queue<int> Queue;
//To know whether reached, so that can stop BFS
bool reached_end = false;
//Visit start node and add to queue
visited[start] = 1;
Queue.push(start);
//BFS until queue is empty
while(!Queue.empty() && !reached_end){
//Pop a node from queue for search operation
int current_node=Queue.front();
Queue.pop();
//Loop through neighbors nodes to find the 'end' node
//add unvisited connected nodes to the queue
int neighbor_node;
while((neighbor_node =unvisitedNeighbor(current_node)) != -1){
//Visit and add neighbor nodes to the queue
visited[neighbor_node] = 1;
Queue.push(neighbor_node);
//update preceding node
prev[neighbor_node] = current_node;
//stop BFS if the end node is found
if(neighbor_node == end){
reached_end = true;
break;
}
}
}
trace_route();
}
//Function returns index of unvisited connected vertices
int unvisitedNeighbor(int index){
for(int i=0; i<N; i++){
if(adjacencyM[index][i] == 1 && (visited[i] == 0)){
return i;
}
}
return -1;
}
//Function to trace back route
void trace_route(){
list<char> route;
int node = end;
//start node has no preceding node
//so loop until prev[node] is -1
while(node != -1){
route.push_front(nodes_name[node]);
node = prev[node];
}
//Display the route
for(char n: route){
cout << n <<" ";
}
}
};
int main()
{
//Driver Code
ShortestPath shortestPath(0, 4);
shortestPath.bfs();
}Java
import java.util.*;
class ShortestPath{
int adjacencyM[][];
char nodes[];
int prev[];
int visited[];
int start, end;
ShortestPath(int adjacencyM[][], char[] nodes, int start, int end){
this.adjacencyM = adjacencyM;
this.nodes = nodes;
this.start = start;
this.end = end;
//array mapping to make visited vertices
this.visited = new int[nodes.length];
//array to store preceding nodes
this.prev = new int[nodes.length];
Arrays.fill(this.prev, -1);
}
public void bfs(){
//Create queue
Queue<Integer> queue = new LinkedList<>();
//Visit and add start node to the queue
visited[start] = 1;
queue.add(start);
//BFS until queue is empty
while(!queue.isEmpty()){
//Pop a node from the queue for search
int current_node = queue.poll();
//Loop through neighbors nodes to find the 'end' node
int neighbor_node;
while((neighbor_node =unvisitedNeighbor(current_node)) != -1){
//visit and add neighbors nodes to the queue
visited[neighbor_node] = 1;
queue.add(neighbor_node);
//update its preceding node
prev[neighbor_node] = current_node;
//End BFS if the end node is found
if(neighbor_node==end){
queue.clear();
break;
}
}
}
//BFS complete, now trace route
trace_route();
}
//Function returns index of unvisited neighbors
private int unvisitedNeighbor(int index){
for(int i=0; i<adjacencyM.length; i++){
if(adjacencyM[index][i] == 1 && visited[i] == 0){
return i;
}
}
return -1;
}
//Function to trace route using preceding nodes
private void trace_route(){
int node = end;
List<Character> route = new ArrayList<>();
//start node has no preceding node
//so loop until prev[node] is -1
while(node!=-1){
route.add(nodes[node]);
node = prev[node];
}
//Reverse route to bring start at front
Collections.reverse(route);
//Output the route
System.out.println(route);
}
}
class Main {
public static void main(String[] args) {
//vertices or nodes array
char nodes[] = {'A', 'B', 'C', 'D', 'E'};
//Adjacency Matrix
int adjacencyM[][] = {{0, 1, 0, 0, 0},
{1, 0, 1, 0, 1},
{0, 1, 0, 1, 1},
{0, 0, 1 ,0, 1},
{0, 1, 0, 1, 0}};
//Driver Code
ShortestPath shortestPath = new ShortestPath(adjacencyM, nodes, 0, 4);
shortestPath.bfs();
}
}Output:
[A, B, E]The worst-case time complexity of the discussed methods is equivalent to the time complexity of the BFS algorithm i.e. O(V+E), where V and E respectively are the numbers of vertices (nodes) and edges of the given graph.
In this tutorial, we learned to find the shortest path in an unweighted graph using the BFS algorithm with Python, C++ and Java programming languages.