Problem: Given a directed graph, check whether it has any cycle or not. A graph with a cycle is also known as cyclic graph.
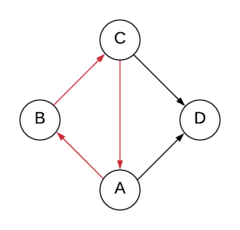
There are several algorithms to detect cycles in a graph. Two of them are bread-first search (BFS) and depth-first search (DFS), using which we will check whether there is a cycle in the given graph.
Detect Cycle in a Directed Graph using DFS
The idea is to traverse the graph along a particular route and check if the vertices of that route form a loop.
If the algorithm repeats any vertices twice when traversing along the same route it means that the given graph has a loop (cycle).
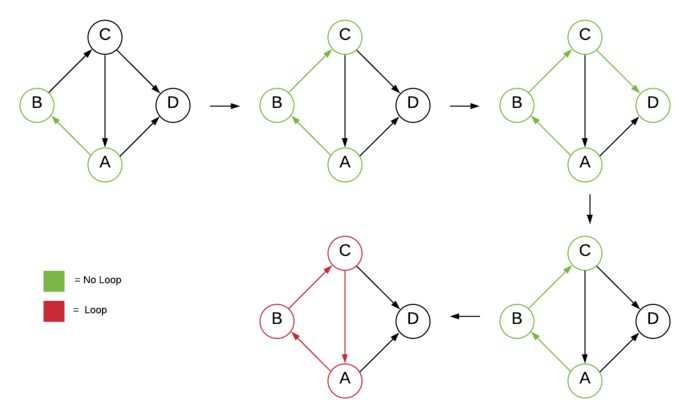
We keep track of vertices in the current route using an additional Boolean flag beingVisited.
In the active route of DFS, all vertices holds beingVisited as true.
So, while traversing a graph using DFS, if we come across any vertex which is already part of the active route (has beingVisited as true), it means there is a loop.
Here is the implementation of the algorithm in C++, Java and Python:
Python
#class representing vertex of a class
class Vertex:
def __init__(self, name):
self.name = name
#variable holds true when visiting is in process
self.beingVisited = False
#variable to mark vertex as visited
self.visited = False
#adjacency list
self.neighbors = []
#method to connect two vertices (undirected)
def add_neighbor(self, vertex):
self.neighbors.append(vertex)
class DFS:
#recursive method to visit vertices of the graph using DFS
def hasCycle(self, vertex):
#start the visiting process
vertex.beingVisited = True;
#go to next connected vertex
for nbr in vertex.neighbors:
#If next vertex is also beingVisited, it means
#there is either self loop or a back edge
if nbr.beingVisited:
return True
#if the following vertex is not visited then visit recursively
#and return true if cycle has been detected
elif not nbr.visited and self.hasCycle(nbr):
return True
#visit process completed
vertex.beingVisited = False;
vertex.visited = True
#return false because current vertex is
#not a part of any cycle
return False
if __name__ == '__main__':
#vertices
vertices = [Vertex('A'), Vertex('B'), Vertex('C'), Vertex('D')]
#connect vertices
vertices[0].add_neighbor(vertices[1]) #A->B
vertices[1].add_neighbor(vertices[2]) #B->C
vertices[2].add_neighbor(vertices[0]) #C->A
vertices[2].add_neighbor(vertices[3]) #C->D
vertices[0].add_neighbor(vertices[3]) #A->D
#driver code
dfs = DFS()
#Extra check for disconnected graph
#so that all graph components are checked
for vertex in vertices:
if dfs.hasCycle(vertex):
print("Has Cycle")
break
else:
print("Doesn't have Cycle")
C++
#include <iostream>
#include <list>
using namespace std;
//class representing a vertex of a graph
class Vertex{
public:
//vertex label
string name;
//variable holds true when visiting is in process
bool beingVisited = false;
//variable to mark vertex as visited
bool visited = false;
//adjacency list
list<Vertex*> neighbors;
Vertex(string name){
this->name = name;
}
//method to connect two vertices (unidirectional)
void add_neighbor(Vertex* vertex){
this->neighbors.push_back(vertex);
}
};
class DFS{
public:
//recursive method to traverse graph (visit vertices) using DFS
//returns true if graph has cycle otherwise false
bool hasCycle(Vertex* vertex){
//start the visiting process
vertex->beingVisited = true;
//go to next connected vertex
for(Vertex* nbr: vertex->neighbors){
//If next vertex is also beingVisited, it means
//there is either self loop or a back edge
if(nbr->beingVisited)
return true;
//if the following vertex is not visited then visit recursively
//and return true if cycle has been detected
else if(!nbr->visited && hasCycle(nbr))
return true;
}
//visit process completed
vertex->beingVisited = false;
vertex->visited = true;
//return false because current vertex is
//not a part of any cycle
return false;
}
};
int main() {
//vertices
Vertex* vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D")};
//connect vertices
vertices[0]->add_neighbor(vertices[1]); //A->B
vertices[1]->add_neighbor(vertices[2]); //B->C
vertices[2]->add_neighbor(vertices[0]); //C->A
vertices[2]->add_neighbor(vertices[3]); //C->D
vertices[0]->add_neighbor(vertices[3]); //A->D
//driver code
DFS dfs;
bool hasCycle = false;
//Extra check for disconnected graph
//so that all graph components are checked
for(Vertex* vertex: vertices){
if(dfs.hasCycle(vertices[0])){
cout << "Has Cycle";
hasCycle = true;
break;
}
}
if(!hasCycle)
cout << "Doesn't have Cycle";
}Java
import java.util.*;
//class representing a vertex of a class
class Vertex{
//vertex label
String name;
//variable holds true when visiting is in process
boolean beingVisited = false;
//variable to mark vertex as visited
boolean visited = false;
//adjacency list
List<Vertex> neighbors= new ArrayList<>();
Vertex(String name){
this.name = name;
}
//method to connect two vertices (unidirectional)
void add_neighbor(Vertex vertex){
this.neighbors.add(vertex);
}
}
class DFS{
//recursive method to traverse graph (visit vertices) using DFS
//returns true if graph has cycle otherwise false
boolean hasCycle(Vertex vertex){
//start the visiting process
vertex.beingVisited = true;
//go to next connected vertex
for(Vertex nbr: vertex.neighbors){
//If next vertex is also beingVisited, it means
//there is either self loop or a back edge
if(nbr.beingVisited)
return true;
//if the following vertex is not visited then visit recursively
//and return true if cycle has been detected
else if(!nbr.visited && hasCycle(nbr))
return true;
}
//visit process completed
vertex.beingVisited = false;
vertex.visited = true;
//return false because current vertex is
//not a part of any cycle
return false;
}
}
class Main {
public static void main(String[] args) {
//vertices
Vertex vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D")};
//connect vertices
vertices[0].add_neighbor(vertices[1]); //A->B
vertices[1].add_neighbor(vertices[2]); //B->C
vertices[2].add_neighbor(vertices[0]); //C->A
vertices[2].add_neighbor(vertices[3]); //C->D
vertices[0].add_neighbor(vertices[3]); //A->D
//driver code
DFS dfs = new DFS();
boolean hasCycle = false;
//Extra check for disconnected graph
//so that all graph components are checked
for(Vertex vertex: vertices){
if(dfs.hasCycle(vertex)){
System.out.println("Has Cycle");
hasCycle = true;
break;
}
}
if(!hasCycle)
System.out.println("Doesn't have Cycle");
}
}
Output:
Has CycleIn the above program ,we have represented the graph using adjacency list.
Since we’re using depth-first traversal, the program’s time complexity is equal to the depth-first search algorithm i.e. O(V+E).
Detect Cycle in a Directed Graph using BFS
We can also check whether the given graph has any cycles or not using the breadth-first search algorithm.
The idea is to traverse the graph using BFS and check any path being repeated. If so, there is a circle in the graph.
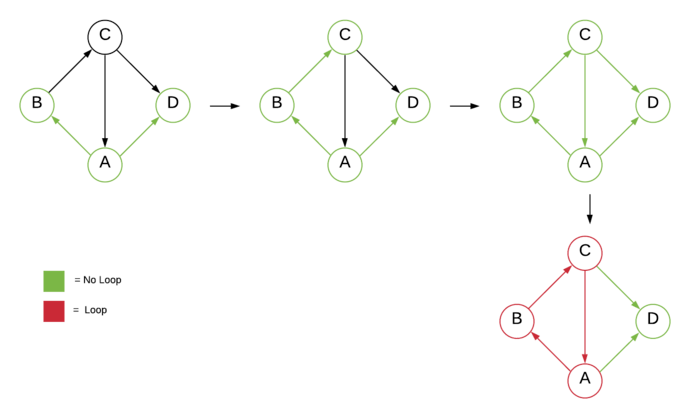
We use an additional Vertex variable (parent) to keep track of traversed paths.
We store the preceding vertex of each vertex into the parent variable.
When traversing the graph using the BFS algorithm, if the next vertex is already visited and the current vertex is its parent, it means we are repeating the same path i.e. the graph has a circle.
Here is the implementation of this approach in C++, Java and Python:
Python
#class representing vertex of a class
class Vertex:
def __init__(self, name):
self.name = name
#variable to hold parent vertex reference
self.parent = None
#variable to mark vertex as visited
self.visited = False
#adjacency list
self.neighbors = []
#method to connect two vertices (undirected)
def add_neighbor(self, vertex):
self.neighbors.append(vertex)
class BFS:
#method to visit vertices of the graph using BFS
#returns true if a cycle is detected otherwise false
def hasCycle(self, start):
#list to be used as a queue
queue = []
#add the start vertex to the queue
queue.append(start)
#mark start vertex as visited
start.visited = True
#parent of start vertex is itself
start.parent = start
#BFS until queue is empty
while queue:
#Pop a vertex from queue to visit
current_vertex = queue.pop(0)
#go to next connected vertex
for nbr in current_vertex.neighbors:
#If next vertex is already Visited and its parent is same as the current vertex
#it means there is either loop or a back edge
if nbr.visited and nbr.parent == current_vertex:
return True
#otherwise add the vertex to the queue,
#mark it visited and update the parent
else:
queue.append(nbr)
#mark visited
nbr.visited = True
nbr.parent = current_vertex.parent
#visited all the vertices of the graph
#no cycle detected, so return false
return False
if __name__ == '__main__':
#vertices
vertices = [Vertex('A'), Vertex('B'), Vertex('C'), Vertex('D')]
#connect vertices
vertices[0].add_neighbor(vertices[1]) #A->B
vertices[1].add_neighbor(vertices[2]) #B->C
vertices[2].add_neighbor(vertices[0]) #C->A
vertices[2].add_neighbor(vertices[3]) #C->D
vertices[0].add_neighbor(vertices[3]) #A->D
#driver code
bfs = BFS()
#Extra check for disconnected graph
#so that all graph components are checked
for vertex in vertices:
if bfs.hasCycle(vertex):
print("Has Cycle")
break
else:
print("Doesn't have Cycle")
C++
#include <iostream>
#include <list>
#include <queue>
using namespace std;
//class representing a vertex of a graph
class Vertex{
public:
//vertex label
string name;
//variable to hold parent vertex reference
Vertex* parent = nullptr;
//variable to mark vertex as visited
bool visited = false;
//adjacency list
list<Vertex*> neighbors;
Vertex(string name){
this->name = name;
}
//method to connect two vertices (unidirectional)
void add_neighbor(Vertex* vertex){
this->neighbors.push_back(vertex);
}
};
class BFS{
public:
//method to visit vertices of the graph using BFS
//returns true if a cycle is detected otherwise false
bool hasCycle(Vertex* start){
//Queue
queue<Vertex*> Queue;
//add the start vertex to the queue
Queue.push(start);
//mark start vertex as visited
start->visited = true;
//parent of start vertex is itself
start->parent = start;
//BFS until queue is empty
while(!Queue.empty()){
//Pop a vertex from queue to visit
Vertex* current_vertex = Queue.front();
Queue.pop();
//go to next connected vertex
for(Vertex* nbr: current_vertex->neighbors){
//If next vertex is already Visited and its parent is same as the current vertex
//it means there is either loop or a back edge
if(nbr->visited && nbr->parent == current_vertex)
return true;
//otherwise add the vertex to the queue,
//mark it visited and update the parent
else{
Queue.push(nbr);
nbr->visited = true;
nbr->parent = current_vertex->parent;
}
}
}
//visited all the vertices of the graph
//no cycle detected, so return false
return false;
}
};
int main() {
//vertices
Vertex* vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D")};
//connect vertices
vertices[0]->add_neighbor(vertices[1]); //A->B
vertices[1]->add_neighbor(vertices[2]); //B->C
vertices[2]->add_neighbor(vertices[0]); //C->A
vertices[2]->add_neighbor(vertices[3]); //C->D
vertices[0]->add_neighbor(vertices[3]); //A->D
//driver code
BFS bfs;
bool hasCycle = false;
//Extra check for disconnected graph
//to ensure all the graph components are checked
for(Vertex* vertex: vertices){
if(bfs.hasCycle(vertices[0])){
cout << "Has Cycle";
hasCycle = true;
break;
}
}
if(!hasCycle)
cout << "Doesn't have Cycle";
}Java
import java.util.*;
//class representing a vertex of a class
class Vertex{
//vertex label
String name;
//variable to hold parent vertex reference
Vertex parent;
//variable to mark vertex as visited
boolean visited = false;
//adjacency list
List<Vertex> neighbors= new ArrayList<>();
Vertex(String name){
this.name = name;
}
//method to connect two vertices (unidirectional)
void add_neighbor(Vertex vertex){
this.neighbors.add(vertex);
}
}
class BFS{
//method to visit vertices of the graph using BFS
//returns true if a cycle is detected otherwise false
boolean hasCycle(Vertex start){
//Queue
Queue<Vertex> queue = new LinkedList<>();
//add the start vertex to the queue
queue.add(start);
//mark start vertex as visited
start.visited = true;
//parent of start vertex is itself
start.parent = start;
//BFS until queue is empty
while(!queue.isEmpty()){
//Pop a vertex from queue to visit
Vertex current_vertex = queue.poll();
//go to next connected vertex
for(Vertex nbr: current_vertex.neighbors){
//If next vertex is already Visited and its parent is same as the current vertex
//it means there is loop
if(nbr.visited && nbr.parent == current_vertex)
return true;
//otherwise add the vertex to the queue,
//mark it visited and update the parent
else{
queue.add(nbr);
nbr.visited = true;
nbr.parent = current_vertex;
}
}
}
//visited all the vertices of the graph
//no cycle detected, so return false
return false;
}
}
class Main {
public static void main(String[] args) {
//vertices
Vertex vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D")};
//connect vertices
vertices[0].add_neighbor(vertices[1]); //A->B
vertices[1].add_neighbor(vertices[2]); //B->C
vertices[2].add_neighbor(vertices[0]); //C->A
vertices[2].add_neighbor(vertices[3]); //C->D
vertices[0].add_neighbor(vertices[3]); //A->D
//driver code
BFS bfs = new BFS();
boolean hasCycle = false;
//Extra check for the disconnected graph
//To ensire all the graph components are checked
for(Vertex vertex: vertices){
if(bfs.hasCycle(vertex)){
System.out.println("Has Cycle");
hasCycle = true;
break;
}
}
if(!hasCycle)
System.out.println("Doesn't have Cycle");
}
}
Output:
Has CycleIn this approach, we add connected vertices to the queue, regardless of whether it was visited or not. That’s because we’re basically searching for a repetition of the path.
The time complexity of this approach is O(V+E) because in the worst-case algorithm will have to detect all the vertices and edges of the given graph.
In this tutorial, we learned to detect cycles in a directed graph using the BFS and DFS traversal algorithm.