Summary: In this tutorial, we will learn what Prim’s minimum spanning tree (lazy version) algorithm is and how can we implement it using languages such as Python, C++, and Java.
What is a Minimum Spanning Tree?
A Minimum Spanning Tree (MST) of any graph is the minimum subsets of edges that can connect all the vertices without forming any cycle and with the minimum total cost.
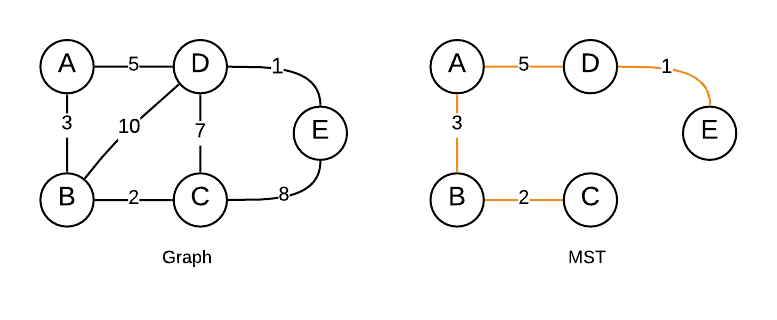
For example, the total cost in the MST of the above graph is 11 and there is no cycle.
Note: A graph can have multiple spanning trees with same minimum total cost.
Prim’s Minimum Spanning Tree Algorithm
Prim’s minimum spanning tree is a greedy algorithm that uses a priority queue to find the MST of the graph.
Priority Queue is a modified version of queue data structure that pops elements based on priority.
It pushes the edges (as it discovers) to the priority queue and fetches them in ascending order of costs to form the MST.
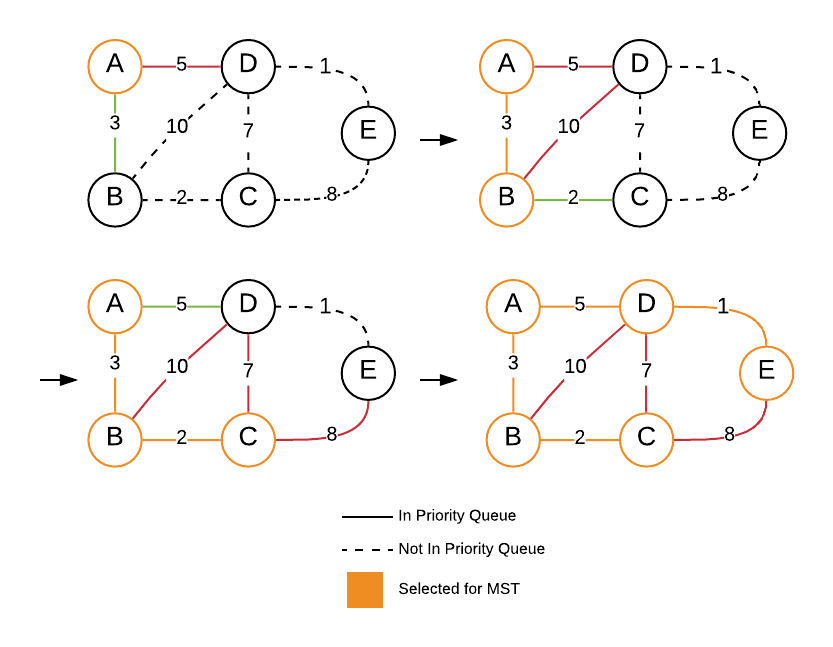
As depicted in the picture, it adds all the edges associated with the source vertex (vertex A) to the priority queue, then selects a low-cost edge using the same to move to the next vertex (vertex B).
The edge which it selects to move to the next vertex becomes a part of the MST.
It repeats the same process at vertex B and moves to vertex C.
At C it discovers two more edges (C—D and C—E) but chooses the edge connecting A and D (A—D) as it the lowest cost among the edges in the priority queue.
At vertex D, the algorithm discovers a final edge (D—E) with a cost of 1 and selects it to complete the MST.
Note: The left out edges are popped out to empty the priority queue.
When all edges are discovered and the priority queue is emptied, the algorithm stops.
How to implement Prim’s algorithm in Programming?
Steps to implement Prim’s Minimum Spanning Tree algorithm:
- Mark the source vertex as visited and add all the edges associated with it to the priority queue.
- While priority queue is not empty and all the edges have not been discovered:
- Pop the least cost edge from the priority queue.
- Check if the target vertex of the popped edge is not have been visited before.
- If so, then add the current edge to the MST.
- Also, mark the target vertex as visited and add all the edges associated with it to the priority queue.
- After the process is complete, check if all the edges were discovered.
- If not, perhaps the graph is cut, and therefore its MST is not possible otherwise, output the MST.
Here is the program that implements the above steps to find the MST of a graph:
Python
from queue import PriorityQueue
class Vertex:
def __init__(self, name):
#vertex label
self.name = name
#edges connected to this vertex
self.edges = []
#visited flag
self.visited = False
#method to connect vertices through bi-directional edges
def connect(self, ad_vertex, edge_cost):
global totalEdges
self.edges.append(Edge(self, ad_vertex, edge_cost))
ad_vertex.edges.append(Edge(ad_vertex, self, edge_cost))
totalEdges += 2
#string representation of the vertex class
def __repr__(self):
return self.name
class Edge:
def __init__(self, _from, _to, _cost):
#from vertex
self._from = _from
#to vertex
self._to = _to
#edge weight or cost
self._cost = _cost
#method to compare two edges (used by the priority queue)
def __lt__(self, other):
if isinstance(other, Edge):
return self._cost < other._cost
return False
#string representation of the edge class
def __repr__(self):
return f"{self._from}-----{self._to}"
class Prims:
def __init__(self):
self.pqueue = PriorityQueue()
self.mst = []
self.totalCost = 0
#function implementing Prim's algorithm
def findMST(self, s):
global totalEdges
#add all edges of the starting vertex
self.addEdges(s)
edgeCount = 0
'''
hunt for low costs edges using PriorityQueue
until all the edges are discovered
'''
while not self.pqueue.empty() and edgeCount != totalEdges:
#pop the low cost edge from PriorityQueue
minEdge = self.pqueue.get()
'''
do not add edges leading to-
already visited vertices
'''
if minEdge._to.visited:
continue
else:
#increment count and add edge to MST
edgeCount += 1
self.totalCost += minEdge._cost
self.mst.append(minEdge)
self.addEdges(minEdge._to)
'''
if not all edges are dicovered, then probalbly the
given graph is dicsconnected, hence MST is not possible.
'''
return edgeCount != totalEdges
#function add edges connected with a vertex to the priority queue
def addEdges(self, s):
s.visited = True;
for edge in s.edges:
if not edge._to.visited:
self.pqueue.put(edge)
if __name__ == '__main__':
#total number of edges
totalEdges = 0
#vertices of the graph
vertices = [Vertex('A'), Vertex('B'), Vertex('C'), Vertex('D'), Vertex('E')]
#connecting vertices
vertices[0].connect(vertices[1], 3)
vertices[0].connect(vertices[3], 5)
vertices[1].connect(vertices[2], 2)
vertices[1].connect(vertices[3], 10)
vertices[2].connect(vertices[3], 7)
vertices[2].connect(vertices[4], 8)
vertices[3].connect(vertices[4], 1)
#driver code
prims = Prims()
if prims.findMST(vertices[0]):
print(prims.mst)
print("Total Cost: ",prims.totalCost)
else:
print("MST not possible for given graph")
C++
#include <iostream>
#include <list>
#include <queue>
using namespace std;
//vertex class prototype
class Vertex;
//total number of edges
int totalEdges = 0;
class Edge{
public:
//from vertex
Vertex* _from;
//to vertex
Vertex* _to;
//edge weight or cost
int _cost;
Edge(Vertex* _from, Vertex* _to, int _cost){
this->_from = _from;
this->_to = _to;
this->_cost = _cost;
}
};
class Vertex{
public:
//vertex label
char name;
//edges connected to this vertex
list<Edge*> edges;
//visited flag
bool visited;
Vertex(char name){
this->name = name;
this->visited = false;
}
//method to connect vertices through bi-directional edges
void connect(Vertex* ad_vertex, int edge_cost){
edges.push_back(new Edge(this, ad_vertex, edge_cost));
edges.push_back(new Edge(ad_vertex, this, edge_cost));
totalEdges += 2;
}
};
/*
*class compares two edges based on their cost
*Will be used by priority queue
*/
class Compare{
public:
bool operator()(Edge *e1, Edge *e2){
return e1->_cost < e2->_cost;
}
};
class Prims{
public:
priority_queue<Edge*, vector<Edge*>, Compare> pqueue;
list<Edge*> mst;
int totalCost= 0;
//function implementing Prim's algorithm
bool findMST(Vertex* s){
//add all edges of the starting vertex
this->addEdges(s);
int edgeCount = 0;
/*
hunt for low cost's edges using PriorityQueue
until all the edges are discovered
*/
while(!this->pqueue.empty() && edgeCount != totalEdges){
//pop the low cost edge from PriorityQueue
Edge* minEdge = this->pqueue.top();
this->pqueue.pop();
/*
do not add edges leading to-
already visited vertices
*/
if(minEdge->_to->visited)
continue;
else{
//increment count and add edge to MST
edgeCount += 1;
this->totalCost += minEdge->_cost;
this->mst.push_back(minEdge);
this->addEdges(minEdge->_to);
}
}
/*
if not all edges are dicovered, then probalbly the
given graph is dicsconnected, hence MST is not possible.
*/
return edgeCount != totalEdges;
}
//function add edges connected with a vertex to the priority queue
void addEdges(Vertex* s){
s->visited = true;
for(Edge* edge: s->edges){
if(!edge->_to->visited)
this->pqueue.push(edge);
}
}
};
int main() {
//total number of edges
totalEdges = 0;
//vertices of the graph
Vertex* vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C'), new Vertex('D'), new Vertex('E')};
//connecting vertices
vertices[0]->connect(vertices[1], 3);
vertices[0]->connect(vertices[3], 5);
vertices[1]->connect(vertices[2], 2);
vertices[1]->connect(vertices[3], 10);
vertices[2]->connect(vertices[3], 7);
vertices[2]->connect(vertices[4], 8);
vertices[3]->connect(vertices[4], 1);
//driver code
Prims prims;
if(prims.findMST(vertices[0])){
for(Edge* edge: prims.mst){
cout << edge->_from->name << "----" << edge->_to->name << "\n";
}
cout << "Total Cost: " << prims.totalCost;
}
else
cout << "MST not possible for given graph";
}Java
import java.util.*;
class Edge implements Comparable<Edge>{
//from vertex
Vertex _from;
//to vertex
Vertex _to;
//edge weight or cost
int _cost;
//total number of edges in the graph
static int totalEdges = 0;
//constructor
Edge(Vertex _from, Vertex _to, int _cost){
this._from = _from;
this._to = _to;
this._cost = _cost;
}
/*
*function compares two edges based on their cost
*Will be used by the priority queue
*/
@Override
public int compareTo(Edge e) {
return (int) (this._cost - e._cost);
}
@Override
public String toString(){
return this._from.name+"----"+this._to.name;
}
}
class Vertex{
//vertex label
char name;
//edges connected to this vertex
List<Edge> edges;
//visited flag
boolean visited;
Vertex(char name){
this.name = name;
this.visited = false;
this.edges = new ArrayList<>();
}
//method to connect vertices through bi-directional edges
void connect(Vertex ad_vertex, int edge_cost){
edges.add(new Edge(this, ad_vertex, edge_cost));
edges.add(new Edge(ad_vertex, this, edge_cost));
Edge.totalEdges += 2;
}
}
class Prims{
PriorityQueue<Edge> pqueue = new PriorityQueue<>();
List<Edge> mst = new ArrayList<>();
int totalCost= 0;
//function implementing Prim's algorithm
boolean findMST(Vertex s){
//add all edges of the starting vertex
this.addEdges(s);
int edgeCount = 0;
/*
hunt for low cost's edges using PriorityQueue
until all the edges are discovered
*/
while(!this.pqueue.isEmpty() && edgeCount != Edge.totalEdges){
//pop the low cost edge from PriorityQueue
Edge minEdge = this.pqueue.peek();
this.pqueue.poll();
/*
do not add edges leading to-
already visited vertices
*/
if(minEdge._to.visited)
continue;
else{
//increment count and add edge to MST
edgeCount += 1;
this.totalCost += minEdge._cost;
this.mst.add(minEdge);
this.addEdges(minEdge._to);
}
}
/*
if not all edges are dicovered, then probalbly the
given graph is dicsconnected, hence MST not possible.
*/
return edgeCount != Edge.totalEdges;
}
//function add edges connected with a vertex to the priority queue
void addEdges(Vertex s){
s.visited = true;
for(Edge edge: s.edges){
if(!edge._to.visited)
this.pqueue.add(edge);
}
}
}
class Main {
public static void main(String[] args) {
//vertices of the graph
Vertex vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C'), new Vertex('D'), new Vertex('E')};
//connecting vertices
vertices[0].connect(vertices[1], 3);
vertices[0].connect(vertices[3], 5);
vertices[1].connect(vertices[2], 2);
vertices[1].connect(vertices[3], 10);
vertices[2].connect(vertices[3], 7);
vertices[2].connect(vertices[4], 8);
vertices[3].connect(vertices[4], 1);
//driver code
Prims prims= new Prims();
if(prims.findMST(vertices[0])){
System.out.println(prims.mst);
System.out.println("Total Cost: "+ prims.totalCost);
}
else{
System.out.println("MST not possible for given graph");
}
}
}Output:
[A—-B, B—-C, A—-D, D—-E]
Total Cost: 11
In the above programs, we specifically define the priority (priorities low-cost edges) of the edges using the __lt__ method in Python, Compare class in C++ and Comparable interface in Java.
Overview of the Prim’s Algorithm
Prim’s Minimum Spanning Tree algorithm works well on the dense graph but fails when the graph is disconnected.
The algorithm has a runtime of O(E*log(E)) (lazy) which can be optimized (eager) to make it more time efficient.