Summary: In this tutorial, we will learn what is Ford Fulkerson Algorithm and how to use Ford Fulkerson Algorithm to find the max flow of a graph.
What is Max Flow?
Given a graph representing a flow network in which one of the vertices is considered as a source (where the flow starts) and another single vertex as a sink (where the flow ends).
Each edge has some specific capacity which represents the maximum allowed flow through it.
We need to find the maximum possible flow from the source to the sink in the given graph network.
The maximum possible flow value is known as max flow.
Tip: Consider each edge as water pipe with a specific width (capacity in case of the graph). We need to find the maximum flow of water from source to sink in the given pipe network (Pipe with larger width/capacity will allow large flow).
Introduction to Ford Fulkerson Algorithm
The Ford–Fulkerson method or the Ford–Fulkerson algorithm (FFA) is a greedy algorithm that computes the maximum flow in a flow network.
Wikipedia
Ford Fulkerson Algorithm helps in finding the max flow of the graph.
In the Ford-Fulkerson method, we repeatedly find the augmenting path through the residual graph and augment the flow until no more augmenting paths can be found.
Residual Graph: It is the given original graph but with the extra equal number of opposite edges as total original edges in the original graph. The capacity of each opposite edge is 0.
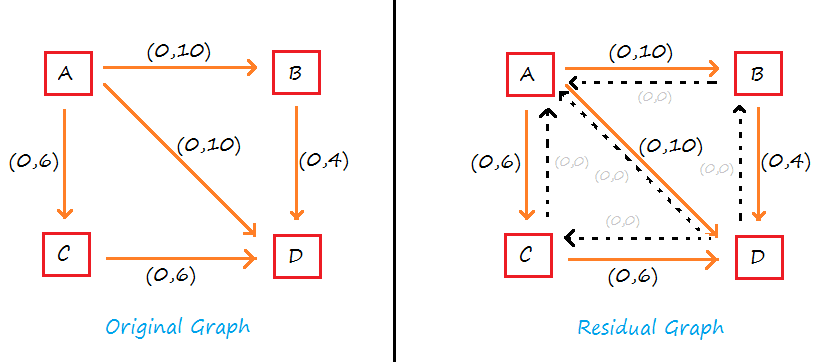
Each Edge has (flow, Capacity) and initially flow = 0.
Augmenting Path: It is the path of edges in which the unused capacity is greater than 0 i.e the flow from source to sink is possible through this path.
Augment the path: Means updating the flow value of the edges along the augmenting path.
On getting any augmenting path we update the residual graph ( i.e update flow of edges in the path found). Again we recheck for augmenting path in the updated graph. If found any, then means that more amount can flow through the network graph. Hence we add the possible flow of the augmenting path to the max flow.
InShort: Repeatedly find the path through which the flow from source to sink is possible and update the flow of the graph until no such path is still left.
Java Program to Implement Ford Fulkerson Algorithm
Before starting program first we need to know how to make a network graph in a programming language.
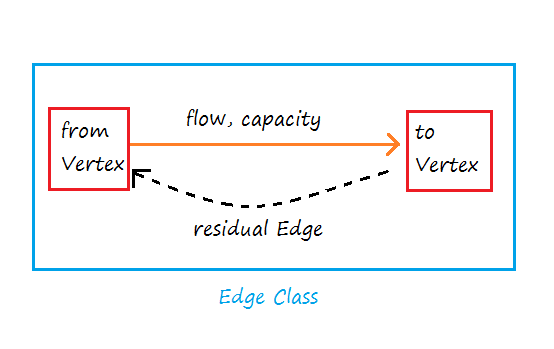
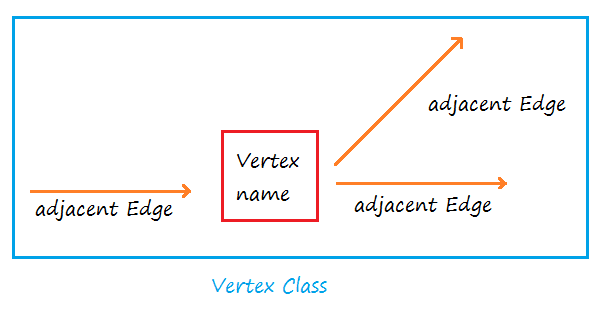
For this, we first need to make Edge and Vertex class. Each Edge class object will represent a different edge and each Vertex class object will represent a different vertex.
So each Edge will have:
Similarly, each Vertex will have:
So we need to create objects of Vertex and Edge class depending on the size of the graph and connect them with each other to make complete network graph.
The Ford Fulkerson algorithm is not applicable to the original graph, we need to create the residual graph of the original graph by creating opposite residual edges for each original edges.
Remember: Initially flow for all edges is 0 and capacity of residual edges should be 0.
Now apply Ford Fulkerson algorithm until no argument path is left.
Note: Backtracking is used to find the augmenting path in the residual graph.
import java.util.ArrayList;
import java.util.List;
public class Vertex {
String name;
List<Edge> adjacentEdges;
int currentVisit;
public Vertex(String name) {
this.name = name;
this.adjacentEdges = new ArrayList<>();
this.currentVisit = 0;
}
public void addNeighbour(Edge edge){
adjacentEdges.add(edge);
}
}
public class Edge {
Vertex fromVertex;
Vertex toVertex;
double capacity;
double flow;
Edge residual;
public Edge(Vertex s, Vertex t, double c){
this.fromVertex = s;
this.toVertex = t;
this.capacity =c;
}
private boolean isResidual(){
return capacity == 0;
}
public double remainingCapacity(){
return capacity - flow;
}
//Augment path/edge
public void augment(double bottleneck){
//Updating the flow of the edge
flow += bottleneck;
//Decreasing the flow of the residual/opposite edge
residual.flow -= bottleneck;
}
}
public class FordFulkerson {
Vertex source;
Vertex sink;
int visitedToken;
double maxFlow;
//Setting Source & Sink
public FordFulkerson(Vertex source, Vertex sink){
this.source =source;
this.sink = sink;
this.visitedToken =0;
this.maxFlow = 0;
}
//Solve For max flow using Ford Fulkerson Method
public void solve(){
visitedToken =1;
//Assuming initially that infinity amount can flow through the network
double flow = Double.MAX_VALUE;
//Finding augment path until there is none left
do{
//If returned value of flow is not 0 then there is augment path
flow = hasAugmentPath(flow, source);
//Adding flow to calculate max flow
maxFlow += flow;
visitedToken++; //Updating visited token for next check
}
while(flow != 0);
}
private double hasAugmentPath(double flow, Vertex vertex) {
//If current Vertex is sink then we reached the target
//It means flow is possible, so return possible flow
if(vertex == sink)
return flow;
//Updating the current visit of the vertex to visitedToken
//So that we do visit the same vertex again
vertex.currentVisit =visitedToken;
//Checking if flow can be continued through any connected adjacentEdges
//Flow can only be continued if remaining capacity of edges is > 0
for(Edge edge: vertex.adjacentEdges){
if(edge.remainingCapacity() > 0 && edge.toVertex.currentVisit != visitedToken){
//Checking min of flow and remaining capacity
//If remaining capacity == 0, then min will be 0
//It means no more flow is possible through the network
double bottleneck = hasAugmentPath(Double.min(flow,edge.remainingCapacity()),edge.toVertex);
//By Backtracking we augment each edge if there is any flow possible
if(bottleneck > 0){
edge.augment(bottleneck);
return bottleneck;
}
}
}
//Returning 0 if no flow is possible through any connected egdes
return 0;
}
}
public class App {
public static void main(String args[]){
//Creating Vertexs
List<Vertex> vertexs = new ArrayList<>();
vertexs.add(new Vertex("A")); //0
vertexs.add(new Vertex("B")); //1
vertexs.add(new Vertex("C")); //2
vertexs.add(new Vertex("D")); //3
//Creating Edges
List<Edge> edges = new ArrayList<>();
edges.add(new Edge(vertexs.get(0),vertexs.get(1),10));
edges.add(new Edge(vertexs.get(1),vertexs.get(3),4));
edges.add(new Edge(vertexs.get(2),vertexs.get(3),6));
edges.add(new Edge(vertexs.get(0),vertexs.get(2),6));
edges.add(new Edge(vertexs.get(2),vertexs.get(1),10));
//Edges and vertices are created but not connected
for(Edge edge: edges){
//Creating opposite edge
Edge opposite = new Edge(edge.toVertex,edge.fromVertex,0);
edge.residual = opposite;
opposite.residual = edge;
//Connecting vertices with edges and residual edges
edge.fromVertex.addNeighbour(edge);
edge.toVertex.addNeighbour(opposite);
}
//Source - 0 -> A
//Sink - 3 -> D
FordFulkerson fordFulkerson = new FordFulkerson(vertexs.get(0),vertexs.get(3));
fordFulkerson.solve();
System.out.println("Max Flow:"+fordFulkerson.maxFlow);
}
}The augment method in the edge class updates the flow of the current edge and deduce the flow of the residual edge.
Remember: Residual edge of the original edge is the opposite edge and the residual edge of the opposite edge is the original edge. So in augment, we increase the flow value of the current edge (can be original or opposite edge) and decrease the flow of the corresponding residual edge.
Max Flow is the sum of all possible flow of the augmenting paths.
Output
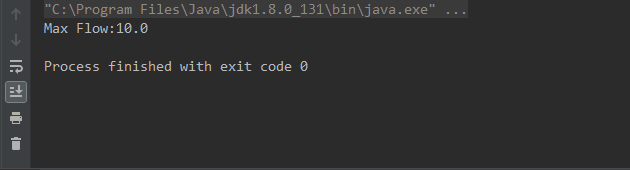
It is possible that you may understand this algorithm or program in one go. Give it few try and watch the video again. You will surely start getting the idea how this algorithm works.
In this tutorial, we learned what Ford Ford Fulkerson algorithm is and how to implement Ford Fulkerson Algorithm to find max flow of a network in Java.