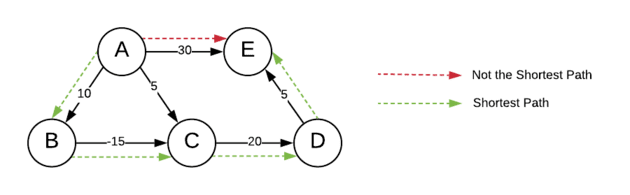
Problem: Given a weighted directed graph, find the shortest path from a given source to a given destination vertex using the Bellman-Ford algorithm.
In the previous post, we learned to calculate the distance of vertices by applying the Bellman-Ford algorithm, did not find the leading path to them.
We can keep track of the path from the source to all other vertices by storing the reference of the preceding vertices.
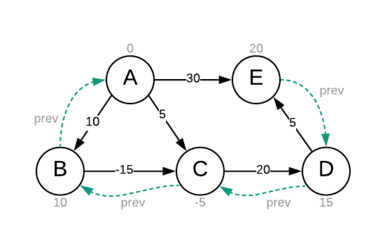
Whenever we relax any edge, we also update the preceding vertex of the target vertex.
By tracing the preceding references, we print the path from the destination to the source node in reverse order.
Here is the implementation of the solution in Python, Java and C++:
Python
class Vertex:
def __init__(self, name):
#vertex label
self.name = name
#distance from the source vertex
self.distance = float('inf')
#predecing vertex
self.prev = None
#string representation of the class
def __repr__(self):
return self.name
class Edge:
def __init__(self, _from, _to, _cost):
#from vertex
self._from = _from
#to vertex
self._to = _to
#edge weight or cost
self._cost = _cost
class BellmanFord:
#method implementing the Bellman-Ford algorithm
def findPath(self, source, edges, v):
#distance of the source vertex to itself is 0
source.distance = 0
#relax all the edges V-1 times
for i in range(v-1):
for edge in edges:
if edge._from.distance + edge._cost < edge._to.distance:
edge._to.distance = edge._from.distance + edge._cost
#update the preceding vertex of the target vertex
edge._to.prev = edge._from
#If any more relaxation is possible
#then, it means graph has a cycle
for edge in edges:
if edge._from.distance + edge._cost < edge._to.distance:
print("Graph has a negative cycle")
return False
return True
'''
function to trace path from destination to
the source vertex using the preceding nodes
'''
def trace_path(self, source, destination):
vertex = destination
path = []
#iterate until we reach the source vertex
while(vertex is not source):
#append vertex to the front of the list
path.insert(0, vertex)
#update the iteration variable
vertex = vertex.prev
#also append the source vertex
path.insert(0, source)
#return the path
return path
if __name__ == '__main__':
#vertices of the graph
vertices = [Vertex('A'), Vertex('B'), Vertex('C'), Vertex('D'), Vertex('E')]
#edges of the graph
edges = [Edge(vertices[0], vertices[1], 10),
Edge(vertices[1], vertices[2], -15),
Edge(vertices[0], vertices[2], 5),
Edge(vertices[2], vertices[3], 20),
Edge(vertices[3], vertices[4], 5),
Edge(vertices[0], vertices[4], 30)]
#driver code
bellmanFord = BellmanFord()
#output the path only when the graph has no cycle
if bellmanFord.findPath(vertices[0], edges, len(vertices)):
print("Distance: ",vertices[4].distance)
print("Path: ", bellmanFord.trace_path(vertices[0], vertices[4]))
C++
#include <iostream>
#include <limits>
#include <list>
using namespace std;
class Vertex{
public:
//vertex label
char name;
//distance from the source vertex
double distance;
//preceding vertex
Vertex* prev = nullptr;
Vertex(char name){
this->name = name;
this->distance = numeric_limits<double>::infinity();
}
};
class Edge{
public:
//from vertex
Vertex* from;
//to vertex
Vertex* to;
//edge weight or cost
double cost;
Edge(Vertex *from, Vertex* to, double cost){
this->from = from;
this->to = to;
this->cost = cost;
}
};
class BellmanFord{
public:
/*
*method implementing Bellman Ford algorithm
*/
bool findPath(Vertex* source, list<Edge*> edges, int v){
//distance of the source vertex to itself is 0
source->distance = 0;
//relax all the edges V-1 times
for(int i=1; i<=(v-1); i++){
for(Edge* edge: edges){
if(edge->from->distance + edge->cost < edge->to->distance){
edge->to->distance = edge->from->distance + edge->cost;
/*
*if edge is relaxed then also update
*the preceding vertex of the target vertex
*/
edge->to->prev = edge->from;
}
}
}
/*
*If any more relaxation is possible
*then, it means graph has a cycle
*/
for(Edge* edge: edges){
if(edge->from->distance + edge->cost < edge->to->distance){
cout << "Graph has a negative cycle";
return false;
}
}
return true;
}
/*
*function to trace path from destination to
*the source vertex using the preceding nodes
*/
list<Vertex*> trace_path(Vertex* source, Vertex* destination){
Vertex* vertex = destination;
list<Vertex*> path;
//iterate until we reach the source vertex
while(vertex != source){
//append vertex to the front of the list
path.push_front(vertex);
//update the iteration variable
vertex = vertex->prev;
}
//also append the source vertex
path.push_front(source);
//return the path
return path;
}
};
int main() {
//vertices of the graph
Vertex* vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C'), new Vertex('D'), new Vertex('E')};
//edges of the graph
list<Edge*> edges {new Edge(vertices[0], vertices[1], 10),
new Edge(vertices[1], vertices[2], -15),
new Edge(vertices[0], vertices[2], 5),
new Edge(vertices[2], vertices[3], 20),
new Edge(vertices[3], vertices[4], 5),
new Edge(vertices[0], vertices[4], 30)};
//driver code
BellmanFord bellmanFord;
/*
*output the path only when the graph has no cycle,
*call the findpath method with V=5
*/
if(bellmanFord.findPath(vertices[0], edges, 5)){
//get the path using the trace_path method
list<Vertex*> path = bellmanFord.trace_path(vertices[0], vertices[4]);
//output the destination vertex distance
cout << "Distance: " << vertices[4]->distance << "\n";
//output the path
cout << "Path: ";
for(Vertex* v: path){
cout << v->name << " ";
}
}
}Java
import java.util.*;
class Vertex{
//vertex label
String name;
//distance from the source vertex
double distance;
//preceding vertex
Vertex prev;
Vertex(String name){
this.name = name;
this.distance = Double.POSITIVE_INFINITY;
}
//string representation of the class
public String toString(){
return this.name;
}
}
class Edge{
//from vertex
Vertex from;
//to vertex
Vertex to;
//edge weight or cost
double cost;
Edge(Vertex from, Vertex to, double cost){
this.from = from;
this.to = to;
this.cost = cost;
}
}
class BellmanFord{
//method implementing Bellman Ford algorithm
boolean findPath(Vertex source, Edge edges[], int v){
//distance of the source vertex to itself is 0
source.distance = 0;
//relax all the edges V-1 times
for(int i=1; i<=(v-1); i++){
for(Edge edge: edges){
if(edge.from.distance + edge.cost < edge.to.distance){
edge.to.distance = edge.from.distance + edge.cost;
/*
*if edge is relaxed then also update
*the preceding vertex of the target vertex
*/
edge.to.prev = edge.from;
}
}
}
/*
*If any more relaxation is possible
*then, it means graph has a cycle
*/
for(Edge edge: edges){
if(edge.from.distance + edge.cost < edge.to.distance){
System.out.println("Graph has a negative cycle");
return false;
}
}
return true;
}
/*
*function to trace path from destination to
*the source vertex using the preceding nodes
*/
List<Vertex> trace_path(Vertex source, Vertex destination){
Vertex vertex = destination;
List<Vertex> path = new ArrayList<>();
//iterate until we reach the source vertex
while(vertex != source){
//append vertex to the front of the list
path.add(0, vertex);
//update the iteration variable
vertex = vertex.prev;
}
//also append the source vertex
path.add(0, source);
//return the path
return path;
}
}
class Main {
public static void main(String[] args) {
//vertices of the graph
Vertex vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D"), new Vertex("E")};
//edges of the graph
Edge edges[] = {new Edge(vertices[0], vertices[1], 10),
new Edge(vertices[1], vertices[2], -15),
new Edge(vertices[0], vertices[2], 5),
new Edge(vertices[2], vertices[3], 20),
new Edge(vertices[3], vertices[4], 5),
new Edge(vertices[0], vertices[4], 30)};
//driver code
BellmanFord bellmanFord = new BellmanFord();
/*
*output the path only when the graph has no cycle,
*call the findpath method with V=5
*/
if(bellmanFord.findPath(vertices[0], edges, 5)){
//get the path using the trace_path method
List<Vertex> path = bellmanFord.trace_path(vertices[0], vertices[4]);
//output the destination vertex distance
System.out.println("Distance: "+ vertices[4].distance);
//output the path
System.out.println("Path: "+path);
}
}
}Output:
Distance: 20Path: [A, B, C, D, E]
In this example, we have chosen A as the source vertex and E as the destination vertex.
In the above program, we have represented graph as a adjacency list.
We first created the list of vertices and edges of the given graph and then executed the Bellman-Ford algorithm on it.
After the execution of the algorithm, we traced the path from the destination to the source vertex and output the same.
The complexity of the algorithm is O(VE). Since this solution incorporates the Belman-Ford algorithm to find the shortest path, it also works with graphs having negative-weighted edges.