Summary: In this tutorial, we will learn what Kahn’s Topological Sort algorithm is and how to obtain the topological ordering of the given graph using it.
Introduction to Topological Sort
Topological ordering of a directed graph is the ordering of its vertices such that for each directed edge from vertex A to vertex B, vertex A appears before vertex B in the ordering.
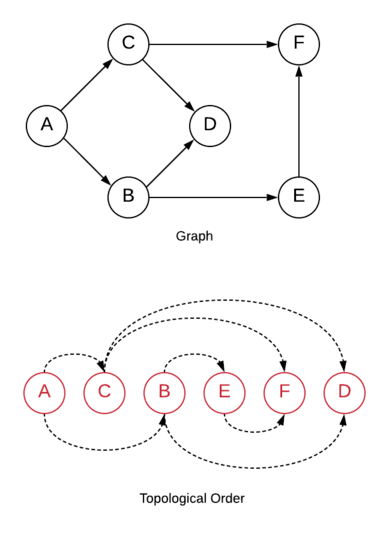
Topological sorting sorts vertices in such a way that every directed edge of the graph has the same direction.
It is important to note that the same graph may have different topological orders.
Topological ordering is only possible for the Directed Acyclic Graphs (i.e., DAG). Graph with cycles cannot be topologically sorted.
Kahn’s Algorithm for Topological Sort
Kahn’s algorithm in order to form topological order constantly looks for the vertices that have no incoming edge and removes all outgoing edges from them.
Basically, the algorithm:
- Finds the vertex that has no incoming edges.
- Remove all outgoing edges from that vertex.
- Add vertex to the topological order.
- Repeat the process until all the vertices are processed.
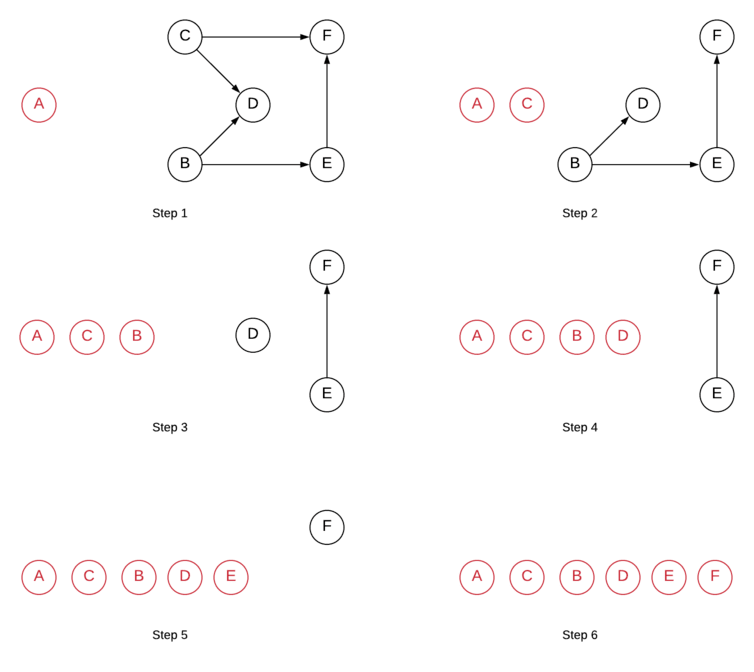
Note: The order may differ depending on which vertices are processed first.
Implementation of the Algorithm
In programming, to perform edge related operations, we use another graph property known as a degree.
A degree to a vertex is the number of incoming edges.
A degree represents how many incoming edges does a vertex has. A vertex with 0 degrees means no incoming edges.
We use Queue to process those vertices because it follows the First In First Out (FIFO) pattern.
To implement Kahn’s Topological Algorithm:
- We look for 0-degree vertices in the given graph and add them to the queue.
- We process the vertices one by one until the queue is emptied.
- We pop a vertex from the queue and add it in topological order.
- After that, we decrement the degree of all its adjacent vertices (apparently to remove the outgoing edges).
- We add it to the queue if the degree of any adjacent vertex is reduced to zero.
- Once all the vertices are processed, we print the order.
Here is the implementation of the algorithm in Python, C++ and Java:
Python
#class representing vertex of the graph
class Vertex:
def __init__(self, name):
#vertex label
self.name = name
#adjacency list
self.neighbors = []
#degree of the vertex
self.degree = 0
#method to add vertex to the adjacency list
#i.e., connect vertices (undirected)
def add_neighbor(self, vertex):
self.neighbors.append(vertex)
#string representation of the class
def __repr__(self):
return self.name
class KahnsTopological:
def __init__(self, vertices):
self.vertices = vertices
#method to initialize degree of every vertices
def init_degree(self):
for vertex in self.vertices:
for nbr in vertex.neighbors:
nbr.degree += 1
#method to find the topological order of the graph
#using the kahn's Topological sort algorithm
def sort(self):
#create an empty queue
queue = []
#fill queue with 0 degree vertices
for vertex in self.vertices:
if vertex.degree == 0:
queue.append(vertex)
#list to store topological order
order = []
#To store count of processed vertices
count = 0
#run the algorithm until queue is empty
while queue:
#dequeue an vertex from the queue
#and append to the order
current_vertex = queue.pop(0)
order.append(current_vertex)
#decrement the degree of the connected vertices
for nbr in current_vertex.neighbors:
nbr.degree -= 1
#if the degree reduces to 0
#add it to the queue
if nbr.degree == 0:
queue.append(nbr)
count =+ 1
#algorithm has finished
#if the number of processed vertices is greater-
#than the number of vertices in the graph,
#then it means the graph has a cycle
if count > len(self.vertices):
print("The graph has cycle")
else:
#output the topological order
print(order)
if __name__ == '__main__':
#vertices
vertices = [Vertex('A'), Vertex('B'), Vertex('C'), Vertex('D'), Vertex('E'), Vertex('F')]
#connect nodes (i.e. create graph)
vertices[0].add_neighbor(vertices[2]); #A->C
vertices[0].add_neighbor(vertices[1]); #A->B
vertices[1].add_neighbor(vertices[3]); #B->D
vertices[2].add_neighbor(vertices[3]); #C->D
vertices[1].add_neighbor(vertices[4]); #B->E
vertices[2].add_neighbor(vertices[5]); #C->F
vertices[4].add_neighbor(vertices[5]); #E->F
#driver code
topological = KahnsTopological(vertices)
topological.init_degree()
topological.sort()
C++
#include <iostream>
#include<list>
#include<queue>
using namespace std;
//class representing a vertex of the graph
class Vertex{
public:
//vertex label
char name;
//Adjacency List
list<Vertex*> neighbors;
//degree of the vertex
int degree = 0;
Vertex(char name){
this->name = name;
}
//Method to connect vertices (directed)
void add_neighbor(Vertex* v){
this->neighbors.push_back(v);
}
};
class KahnsTopological{
public:
Vertex** vertices;
int n;
KahnsTopological(Vertex* vertices[], int n){
this->vertices = vertices;
this->n = n;
}
//method to initialize degree of every vertices
void init_degree(){
for(int i=0; i<n; i++){
Vertex* vertex= vertices[i];
for(Vertex* nbr: vertex->neighbors){
nbr->degree += 1;
}
}
}
//method to find the topological order of the graph
//using the kahn's Topological sort algorithm
void sort(){
//create an empty queue
queue<Vertex*> Queue;
//fill queue with 0 degree vertices
for(int i=0; i<n; i++){
Vertex* vertex= vertices[i];
if(vertex->degree == 0)
Queue.push(vertex);
}
//list to store topological order
list<Vertex*> order;
//To store count of processed vertices
int count = 0;
//run the algorithm until queue is empty
while(!Queue.empty()){
//dequeue an vertex from the queue
//and append to the order
Vertex* current_vertex = Queue.front();
Queue.pop();
order.push_back(current_vertex);
//decrement the degree of the connected vertices
for(Vertex* nbr: current_vertex->neighbors){
nbr->degree -= 1;
//if the degree reduces to 0
//add it to the queue
if(nbr->degree == 0)
Queue.push(nbr);
}
count++;
}
//algorithm has finished
//if the number of processed vertices is greater-
//than the number of vertices in the graph,
//then it means the graph has a cycle
if(count > n)
cout << "The graph has cycle";
else{
//output the topological order
for(Vertex* v: order){
cout << v->name << " ";
}
}
}
};
int main()
{
//vertices
Vertex* vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C'), new Vertex('D'), new Vertex('E'), new Vertex('F')};
//connect vertices (i.e. create graph)
vertices[0]->add_neighbor(vertices[1]); //A->B
vertices[0]->add_neighbor(vertices[2]); //A->C
vertices[1]->add_neighbor(vertices[3]); //B->D
vertices[2]->add_neighbor(vertices[3]); //C->D
vertices[1]->add_neighbor(vertices[4]); //B->E
vertices[2]->add_neighbor(vertices[5]); //C->F
vertices[4]->add_neighbor(vertices[5]); //E->F
//Driver Code
KahnsTopological topological(vertices, 6);
topological.init_degree();
topological.sort();
}Java
import java.util.*;
//class representing a vertex of the graph
class Vertex{
//vertex label
String name;
//degree of the vertex
int degree = 0;
//Adjacency List
List<Vertex> neighbors = new ArrayList<>();
Vertex(String name){
this.name = name;
}
//Method to connect vertices (directed)
public void add_neighbor(Vertex v){
this.neighbors.add(v);
}
public String toString(){
return this.name;
}
};
class KahnsTopological{
Vertex vertices[];
KahnsTopological(Vertex vertices[]){
this.vertices = vertices;
}
//method to initialize degree of every vertices
void init_degree(){
for(Vertex vertex: vertices){
for(Vertex nbr: vertex.neighbors){
nbr.degree += 1;
}
}
}
//method to find the topological order of the graph
//using the kahn's Topological sort algorithm
void sort(){
//create an empty queue
Queue<Vertex> queue = new LinkedList<>();
//fill queue with 0 degree vertices
for(Vertex vertex: vertices){
if(vertex.degree == 0)
queue.add(vertex);
}
//list to store topological order
List<Vertex> order = new ArrayList<>();
//To store count of processed vertices
int count = 0;
//run the algorithm until queue is empty
while(!queue.isEmpty()){
//dequeue an vertex from the queue
//and append to the order
Vertex current_vertex = queue.poll();
order.add(current_vertex);
//decrement the degree of the connected vertices
for(Vertex nbr: current_vertex.neighbors){
nbr.degree -= 1;
//if the degree reduces to 0
//add it to the queue
if(nbr.degree == 0)
queue.add(nbr);
}
count++;
}
//algorithm has finished
//if the number of processed vertices is greater-
//than the number of vertices in the graph,
//then it means the graph has a cycle
if(count > vertices.length)
System.out.println("The graph has cycle");
else{
//output the topological order
System.out.println(order);
}
}
}
class Main {
public static void main(String[] args) {
//vertices
Vertex vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D"), new Vertex("E"), new Vertex("F")};
//connect vertices (i.e. create graph)
vertices[0].add_neighbor(vertices[1]); //A->B
vertices[0].add_neighbor(vertices[2]); //A->C
vertices[1].add_neighbor(vertices[3]); //B->D
vertices[2].add_neighbor(vertices[3]); //C->D
vertices[1].add_neighbor(vertices[4]); //B->E
vertices[2].add_neighbor(vertices[5]); //C->F
vertices[4].add_neighbor(vertices[5]); //E->F
//Driver Code
KahnsTopological topological = new KahnsTopological(vertices);
topological.init_degree();
topological.sort();
}
}Output:
Python: [A, C, B, D, E, F]C++: [A, B, C, E, D, F]
Java: [A, B, C, E, D, F]
The order of different languages is not the same, yet all are correct.
The orders are such that for each directed edge from vertex A to vertex B, vertex A appears before vertex B in the ordering.
In the above programs, the init_degree() method calculates the degree of each vertex of a given graph. We have called this method before the sorting process.
If there is a cycle in the graph, some vertices will be processed several times. In that case, the count of processed vertices exceeds the number of vertices in the graph, and topological order is not possible.
In this tutorial, we learned to get the topological ordering of the vertices of the given graph using the Kahn’s Topological Sort Algorithm