Summary: In this tutorial, we will learn what Topological Sort Algorithm is and how to sort vertices of the given graph using topological sorting.
Introduction to Topological Sort
A topological ordering is an ordering of the vertices in a directed graph where for each directed edge from vertex A to vertex B, vertex A appears before vertex B in the ordering.
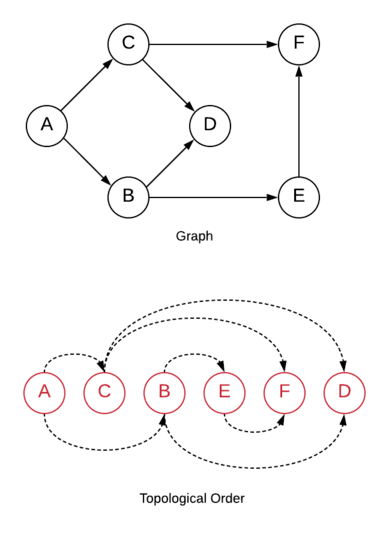
Topological sorting sorts vertices in such a way that every directed edge of the graph has the same direction.
Topological ordering is only possible for the Directed Acyclic Graphs (i.e., DAG). Graph with cycles cannot be topologically sorted.
It is important to note that the same graph may have different topological orders.
Algorithm for Topological Sort
We can sort the vertices of the graph in topological order using the depth-first search algorithm, because in topological ordering, the vertices without any child or neighbor vertex (leaf nodes in case of a tree) comes to the right or at last.
Using DFS, we traverse the graph and add the vertices to the list during its traceback process.
Since the traceback happens from the leaf nodes up to the root, the vertices gets appended to the list in the topological order.
We attach the visited vertices to the front of the list to ensure that the last visited vertices come to the right.
Here is the implementation of the algorithm in Python, C++ and Java:
Python
#class representing a vertex of the graph
class Vertex:
def __init__(self, name):
#vertex label
self.name = name
#variable to mark vertex as visited
self.visited = False
#adjacency list
self.neighbors = []
#Method to connect vertices (directed)
def add_neighbor(self, node):
self.neighbors.append(node)
#String representaion of the class
def __repr__(self):
return self.name
class Topological:
def __init__(self):
#list to store the topological order of vertices
self.order = []
#method to initiate topological sort
def sort(self, vertices):
#iterate through vertices to ensure
#all vertices are visited
for vertex in vertices:
if not vertex.visited:
#visit the vertex using DFS
self.dfs(vertex)
#sorting finished
#print the topological order
print(self.order)
#method implementing DFS
def dfs(self, vertex):
#mark vertex as visited
vertex.visited = True
#recursively visit all neighbors vertices
for nbr in vertex.neighbors:
if not nbr.visited:
self.dfs(nbr)
#recusive traceback
#append vertex to the order in the front
self.order.insert(0, vertex)
if __name__ == '__main__':
#vertices
vertices = [Vertex('A'), Vertex('B'), Vertex('C'), Vertex('D'), Vertex('E'), Vertex('F')]
#connect nodes (i.e. create graph)
vertices[0].add_neighbor(vertices[2]); #A->C
vertices[0].add_neighbor(vertices[1]); #A->B
vertices[1].add_neighbor(vertices[3]); #B->D
vertices[2].add_neighbor(vertices[3]); #C->D
vertices[1].add_neighbor(vertices[4]); #B->E
vertices[2].add_neighbor(vertices[5]); #C->F
vertices[4].add_neighbor(vertices[5]); #E->F
#driver code
topological = Topological()
topological.sort(vertices)
C++
#include <iostream>
#include<list>
using namespace std;
//class representing a vertex of the graph
class Vertex{
public:
//vertex label
char name;
//variable to mark vertex as visited
bool visited = false;
//Adjacency List
list<Vertex*> neighbors;
Vertex(char name){
this->name = name;
}
//Method to connect vertices (directed)
void add_neighbor(Vertex* v){
this->neighbors.push_back(v);
}
};
class Topological{
public:
//list to store the topological order of vertices
list<Vertex*> order;
//method to initiate topological sort
void sort(Vertex* vertices[], int N){
//iterate through vertices to ensure
//all vertices are visited
for(int i=0; i<N; i++){
Vertex* vertex = vertices[i];
if(!vertex->visited){
//visit the vertex using DFS
dfs(vertex);
}
}
//sorting finished
//print the topological order
for(Vertex* vertex: order){
cout << vertex->name << " ";
}
}
//method implementing DFS
void dfs(Vertex* vertex){
//mark vertex as visited
vertex->visited = true;
//recursively visit all neighbors vertices
for(Vertex* nbr: vertex->neighbors){
if(!nbr->visited){
dfs(nbr);
}
}
//recursive traceback
//append vertex to the order on the front
order.push_front(vertex);
}
};
int main()
{
//vertices
Vertex* vertices[] = {new Vertex('A'), new Vertex('B'), new Vertex('C'), new Vertex('D'), new Vertex('E'), new Vertex('F')};
//connect vertices (i.e. create graph)
vertices[0]->add_neighbor(vertices[1]); //A->B
vertices[0]->add_neighbor(vertices[2]); //A->C
vertices[1]->add_neighbor(vertices[3]); //B->D
vertices[2]->add_neighbor(vertices[3]); //C->D
vertices[1]->add_neighbor(vertices[4]); //B->E
vertices[2]->add_neighbor(vertices[5]); //C->F
vertices[4]->add_neighbor(vertices[5]); //E->F
//Driver Code
Topological topological;
topological.sort(vertices, 6);
}Java
import java.util.*;
//class representing a vertex of the graph
class Vertex{
//vertex label
String name;
//variable to mark vertex as visited
boolean visited = false;
//Adjacency List
List<Vertex> neighbors = new ArrayList<>();
Vertex(String name){
this.name = name;
}
//Method to connect vertices (directed)
public void add_neighbor(Vertex v){
this.neighbors.add(v);
}
public String toString(){
return this.name;
}
};
class Topological{
//list to store the topological order of vertices
List<Vertex> order = new ArrayList<>();
//method to initiate topological sort
public void sort(Vertex vertices[]){
//iterate through vertices to ensure
//all vertices are visited
for(Vertex vertex: vertices){
if(!vertex.visited){
//visit the vertex recursively
dfs(vertex);
}
}
//sorting finished
//print the topological order
System.out.println(order);
}
//method implementing DFS
private void dfs(Vertex vertex){
//mark vertex as visited
vertex.visited = true;
//recursively visit all neighbors vertices
for(Vertex nbr: vertex.neighbors){
if(!nbr.visited){
dfs(nbr);
}
}
//recusive traceback
//append vertex to the order in the front
order.add(0, vertex);
}
}
class Main {
public static void main(String[] args) {
//vertices
Vertex vertices[] = {new Vertex("A"), new Vertex("B"), new Vertex("C"), new Vertex("D"), new Vertex("E"), new Vertex("F")};
//connect vertices (i.e. create graph)
vertices[0].add_neighbor(vertices[1]); //A->B
vertices[0].add_neighbor(vertices[2]); //A->C
vertices[1].add_neighbor(vertices[3]); //B->D
vertices[2].add_neighbor(vertices[3]); //C->D
vertices[1].add_neighbor(vertices[4]); //B->E
vertices[2].add_neighbor(vertices[5]); //C->F
vertices[4].add_neighbor(vertices[5]); //E->F
//Driver Code
Topological topological = new Topological();
topological.sort(vertices);
}
}Output:
[A, C, B, E, F, D]In the above programs, we have represented the graph using the adjacency list.
We are appending the vertices (which have been visited) in front of the order list so that the vertices in the list are in the same order as they were visited (i.e., the last visited vertex will come to a final).
The time complexity of the algorithm used is O(V+E) because DFS has to visit all the edges of the graph to create a topological order containing all vertices of the graph.
Application of Topological Sort
Topological sorting is useful in cases where there is a dependency between given jobs or tasks.
For example, if Job B has a dependency on job A then job A should be completed before job B.
For multiple such cases, we treat jobs as entities and sort them using topological sort to get their correct to do order.
Related Topics: