Print Pascal’s Triangle in Java [3 Methods]

Summary: In this programming example, we will learn three different ways to print pascal’s triangle in Java.

Method 1: Pascal’s Triangle using Combination

Each row in Pascal’s triangle is the coefficients of the binomial expansion i.e. ^(row-1)C_(column-1)

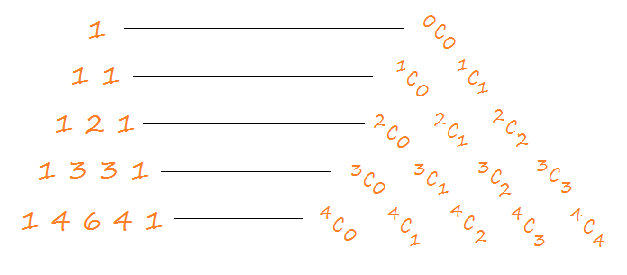
We can easily calculate the value of ^(row-1)C_(column-1) in Java and generate a pascal’s triangle.

All we need to do is to define a function which will return the value of ^(row-1)C_(column-1) for the respective value of row and column.

Here is the implementation of the method in Java:

import java.util.Scanner;
 
class Main {
  public static void main(String[] args) {
 
    Scanner in = new Scanner(System.in);
    System.out.print("Enter value of n: ");
    int n = in.nextInt();
 
    for(int i=0; i<n; i++){
      for(int k=1; k<n-i; k++){
        System.out.print(" ");
      }
      for(int j=0; j<=i; j++){
        System.out.print(nCr(i,j)+" ");
      }
      System.out.println();
    }
    
  }
  //Function to return the value of nCr
  private static int nCr(int n, int r){
    if(n<r || n==0)
      return 1;
 
    int num = 1, den = 1;
    for(int i=r; i>=1; i--){
      num = num * n--;
      den = den * i;
    }
    return num/den;
  }
}

Output:

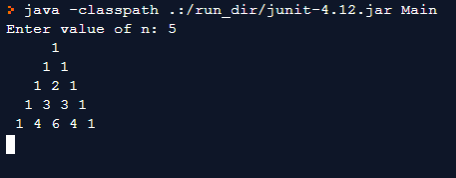
The time complexity of this method is O(n3) because, for each term inside 2 loops, we are calling a combination function which itself uses a for loop to calculate the value of ⁿC_r.

We can reduce the complexity of this program using a 2D array.

Method 2: Pascal’s Triangle using Array

If we notice the triangle carefully we observe that each entry in Pascal’s triangle is the sum of two values of the previous row.

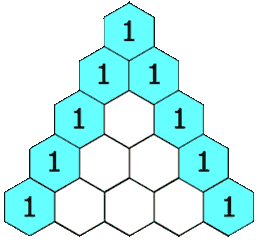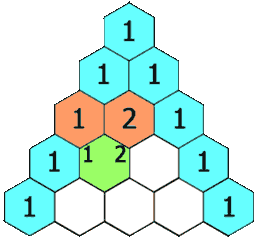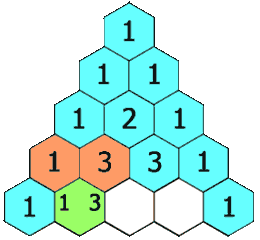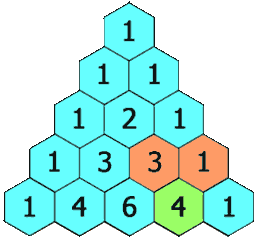
Hence we can use a 2D array to compute and store the value of each term from previously generated values and then output the array which will contain pascal’s triangle’s values.

import java.util.Scanner;
 
class Main {
  public static void main(String[] args) {
 
    Scanner in = new Scanner(System.in);
    System.out.print("Enter value of n: ");
    int n = in.nextInt();
 
    int ncr[][] = new int[n][n];
 
    ncr[0][0] = 1;  //First element is always 1
 
    //start from 2nd row i.e from i=1
    for(int i=1; i<n; i++){
      //First element of each row is always 1
      ncr[i][0] = 1; 
      for(int j=1; j<=i; j++){
        ncr[i][j] = ncr[i-1][j-1] + ncr[i-1][j];
      }
    }
 
    //Output the array
    for(int i=0; i<n; i++){
      //Output the blank space
      for(int k=0; k<n-i; k++){
        System.out.print(" ");
      }
      for(int j=0; j<=i; j++){
        System.out.print(ncr[i][j]+" ");
      }
      System.out.println();
    }
 
  }
}

Output:

The time and space complexity of this method is O(n²) and O(n) respectively.

The space complexity is because of the use of an extra array.

We can reduce the space complexity of this program by not using the array.

Method 3: Pascal Triangle without Array

The formula for each term of Pascal’s triangle except the first and last element of each row (which is always 1) is t=t*(i-j +1)/j

where ‘i’ represent the row, ‘j’ represent the column and ‘t’ represents the last term value.

All we need to do is to check the row and column index of each term inside the nested loop. If it is the first row or first column (i.e. if(j==0 || i==j)) we will simply output 1 otherwise we will output the value of t*(i-j +1)/j.

Here is the implementation of the method in Java:

import java.util.Scanner;
 
class Main {
  public static void main(String[] args) {
 
    Scanner in = new Scanner(System.in);
    System.out.print("Enter value of n: ");
    int n = in.nextInt();
 
    int t=1;
 
    for(int i=0; i<n; i++){
      //Output the blank space
      for(int k=0; k<n-i; k++){
        System.out.print(" ");
      }
      for(int j=0; j<=i; j++){
        if(j==0 || i==j)
          t = 1;
        else
          t=t*(i-j +1)/j;
        
        System.out.print(t+" ");
      }
      System.out.println();
    }
 
  }
}

Output:

The time and space complexity of the above program is O(n²) and O(1) respectively.

In this tutorial, we learned with examples the different ways to print the Pascal’s triangle using Java programming language.