Problem: Write a Java program to find the value of the combination formula i.e. nCr.
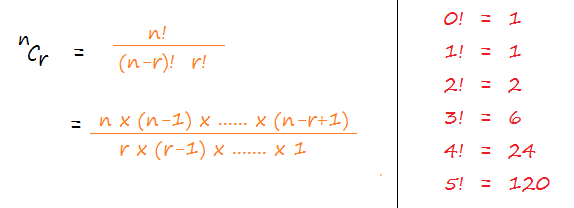
The above formula is used in mathematics to calculate the combination value, and we can use the same in our java program.
Since all the three terms (n!, (n-r)! and r!) in the formula are factorials, we will write a function that will compute factorial for all the three terms and use the same in the formula.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//Enter value of n
System.out.print("Enter n: ");
int n = in.nextInt();
//Enter value of r
System.out.print("Enter r: ");
int r = in.nextInt();
//find nCr using the formula
int combination = factorial(n)/(factorial(n-r)*factorial(r));
System.out.println("nCr: "+combination);
}
//function finds factorial of a number
private static int factorial(int num){
if(num==0 || num==1)
return 1;
int fact = 1;
for(int i=2; i<=num; i++){
fact = fact*i;
}
return fact;
}
}Output:
Enter n: 5
Enter r: 2
nCr: 10
This method is successfully able to calculate the value of nCr however it is not so efficient.
If the value of n is large, the computation of the factorials consumes time.
We can further improve the efficiency of the program by simplifying the formula.
Efficient way to Calculate Combination in Java
The simplified formula (as depicted in the first image) eliminates the need for computing factorial which performs much better than the first formula for large numbers.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//enter the value of n
System.out.print("Enter n: ");
int n = in.nextInt();
//enter the value of r
System.out.print("Enter r: ");
int r = in.nextInt();
//call the function and output the result
System.out.println("nCr: "+nCr(n,r));
}
//function calculates nCr using the simplified formula
private static int nCr(int n, int r){
if(n<r || n==0)
return 1;
int num = 1, den = 1;
for(int i=r; i>=1; i--){
num = num * n--;
den = den * i;
}
return num/den;
}
}Output:
Enter n: 10
Enter r: 3
nCr: 120

We can also use streams
import java.util.Arrays;
import java.util.stream.IntStream;
import java.util.stream.Stream;
public class Testes {
public static void main(String[] args) {
// TODO Auto-generated method stub
//nCr=(n!/((n-r)!*r!))
int n=5;
int r=2;
int dif=n-r;
int fn=factorial(n);
int fdif=factorial(dif);
int fr=factorial(r);
int nropc=fn/(fdif*fr);
System.out.println(nropc);
}
static int factorial(int val) {
int fa=0;
fa=Stream.iterate(val,n->n>=1,v->v-1)
.reduce((a,b)->a*b).get();
return fa;
}
}