Summary: In this tutorial, we will learn what Radix Sort Algorithm is, how it works, and how to sort an array using the Radix Sort algorithm in C, C++, and Java.
Introduction to Radix Sort Algorithm
Radix Sort is a stable form of counting sort algorithm that is used to sort arrays values having the same radix or width.
The algorithm sorts array on the basis of the significant digits i.e. it sorts elements based on from the least significant digit to the most significant digit.
The following picture illustrate the working of Radix Sort Algorithm:
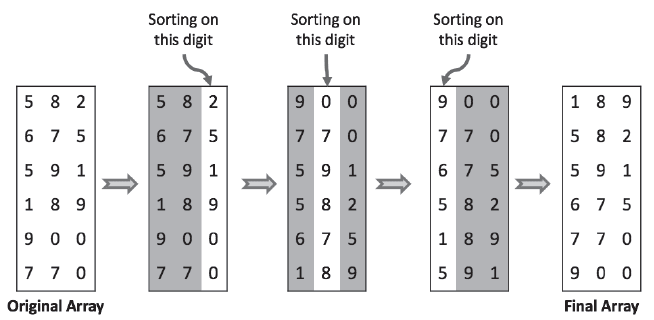
As you can notice the algorithm iteratively sorts array on the basic of the digits.
Here are some important points about radix sort algorithm:
- Radix sort cannot be applied to all types of data. It can only be used with strings and positive integers (Not with Decimal numbers).
- Strings and Integers must have same width. e.g. [22, 54, 69, 85, 45], [8596, 1025, 7456, 1298, 5200] etc. Notice that every element in the respective array has same length/digits/width.
- Sorting starts from the rightmost position.
- Radix sort must use counting sort or any other stable sorting algorithm.
Radix Sort Algorithm
- Sort array elements on the basis of the digits on the 1’s position.
- Then, sort the same array elements on the basis of digits on the 10’s position.
- Again, sort the array elements on the basis of digits on the 100’s position.
- Repeat the process until you are done sorting on the basis of the most significant digits.
- Finally, the array will be sorted.
Note: The above sorting process should be stable i.e. the integers having the same digits should not change position relatively.
Here is the implementation of the radix sort algorithm in C, C++, and Java:
C
#include <stdio.h>
#include <stdlib.h>
void radix_sort(int arr[], int s);
void display(int arr[], int s);
int cal_width(int v);
void init_with_zero(int arr[]);
int main()
{
int arr[] = {582, 675, 591, 189, 900, 770};
printf("Array before sorting \n");
display(arr, 6);
radix_sort(arr, 6);
printf("Array after sorting \n");
display(arr, 6);
return 0;
}
void radix_sort(int arr[], int s){
int power, digit, num, count_array[10];
int temp[s];
init_with_zero(count_array);
int width = cal_width(arr[0]);
for(int i=0; i<width; i++){
power=i;
for(int j=0; j<s; j++){
num = arr[j];
num = num/pow(10,power);
digit = num%10;
count_array[digit]++;
}
for(int j=1; j<10;j++){
count_array[j]=count_array[j-1]+count_array[j];
}
for(int j=5; j>=0;j--){
temp[--count_array[get_digit(arr[j],i+1)]] = arr[j];
}
init_with_zero(count_array);
}
//copying temp (sorted) array to original array
for(int i=0; i<6; i++){
arr[i]= temp[i];
}
}
int cal_width(int v){
int c=0;
while(v != 0){
v=v/10;
c++;
}
return c;
}
void init_with_zero(int arr[]){
for(int i=0; i<10 ; i++)
arr[i] = 0;
}
int get_digit(int a, int p){
while(p != 1){
a=a/10;
p--;
}
return a%10;
}
void display(int arr[], int s){
for(int i=0; i<s ; i++)
printf("%d ",arr[i]);
printf("\n");
}C++
#include <iostream>
#include <cmath>
using namespace std;
void radix_sort(int arr[], int s);
void display(int arr[], int s);
int cal_width(int v);
void init_with_zero(int arr[]);
int main()
{
int arr[] = {582, 675, 591, 189, 900, 770};
cout << "Array before sorting" << endl;
display(arr, 6);
radix_sort(arr, 6);
cout << "Array after sorting" << endl;
display(arr, 6);
return 0;
}
void radix_sort(int arr[], int s){
int i, j, power, digit, num, count_array[10];
int temp[s];
init_with_zero(count_array);
int width = cal_width(arr[0]);
for(i=0; i<width; i++){
power=i;
for(j=0; j<s; j++){
num = arr[j];
num = num/pow(10,power);
digit = num%10;
count_array[digit]++;
}
for(j=1; j<10;j++){
count_array[j]=count_array[j-1]+count_array[j];
}
for(j=5; j>=0;j--){
temp[--count_array[get_digit(arr[j],i+1)]] = arr[j];
}
init_with_zero(count_array);
}
//copying temp (sorted) array to original array
for(i=0; i<6; i++){
arr[i]= temp[i];
}
}
int cal_width(int v){
int c=0;
while(v != 0){
v=v/10;
c++;
}
return c;
}
void init_with_zero(int arr[]){
for(int i=0; i<10 ; i++)
arr[i] = 0;
}
int get_digit(int a, int p){
while(p != 1){
a=a/10;
p--;
}
return a%10;
}
void display(int arr[], int s){
for(int i=0; i<s ; i++)
cout << arr[i] << " ";
cout << endl;
}Java
public class RadixSort {
int arr[];
public RadixSort(int[] arr) {
this.arr = arr;
}
int cal_width(int v){
int c=0;
while(v != 0){
v=v/10;
c++;
}
return c;
}
void init_with_zero(int arr[]){
for(int i=0; i<10 ; i++)
arr[i] = 0;
}
int get_digit(int a, int p){
while(p != 1){
a=a/10;
p--;
}
return a%10;
}
public void sort(){
int i, j, power, digit, num;
int s= arr.length;
int temp[] = new int[s];
int count_array[] = new int[10];
init_with_zero(count_array);
int width = cal_width(arr[0]);
for(i=0; i<width; i++){
power=i;
for(j=0; j<s; j++){
num = arr[j];
num = (int) (num/Math.pow(10,power));
digit = num%10;
count_array[digit]++;
}
for(j=1; j<10;j++){
count_array[j]=count_array[j-1]+count_array[j];
}
for(j=5; j>=0;j--){
temp[--count_array[get_digit(arr[j],i+1)]] = arr[j];
}
init_with_zero(count_array);
}
//copying temp (sorted) array to original array
for(i=0; i<6; i++){
arr[i]= temp[i];
}
}
}
public class App {
public static void main(String args[]){
int arr[] = {582, 675, 591, 189, 900, 770};
System.out.println("Array before sorting");
display(arr);
RadixSort rs = new RadixSort(arr);
rs.sort();
System.out.println("Array after sorting");
display(arr);
}
public static void display(int arr[]){
for(int i=0; i<arr.length ; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}Output:
Array before sorting 582 675 591 189 900 770 Array after sorting 189 582 591 675 770 900
In the above program, we first initialize the elements of the count_array[] with 0 using the init_with_zero(int arr[]) function.
We then calculate the width (i.e. number of significant digits) of the array element using cal_width(int v) function.
Knowing the width we iterate through the significant digits and the array elements and sort them using the counting sort stable algorithm.
The get_digit(int a, int p) function returns the digit of ‘a’ at pth position.
Radix Sort Overview
- In-place algorithm: No extra array is used.
- Stable Algorithm: No interchange of integers having duplicates digits.
- O(n) time complexity: The complexity depends on the width (radix) of the elements.
In this tutorial, we learned what is Radix sort algorithm, how it works and how to sort an array using the Radix Sort Algorithm in C, C++, and Java programming languages.
