Summary: In this tutorial, we will learn from examples what dynamic programming is and how it reduces the timing complexity of the program.
Introduction to Dynamic Programming
Dynamic programming is a way of solving a problem by breaking it down into a collection of subproblems.
In dynamic programming, we store the solution of repetitive subproblems so that they can be reused later in the computation task of the program.
In doing so, we avoid the computation of repetitive tasks which reduces the time taken by the program to solve a given problem.
In short, Dynamic programming optimizes code for the better execution and performance of the program.
It reduces the time complexity of the algorithm or program (i.e. the method takes far less time than the approach which does not take advantages of dynamic programming).
Let’s see an example for a better understanding.
Example:
Consider the following naive recursive program which computes the nth Fibonacci number:
int naiveFibonacci(int n){
if(n==0 || n==1)
return n;
return naiveFibonacci(n-1) + naiveFibonacci(n-2);
}In this approach, on every function call, there will be a further two recursive calls.
Therefore, it may happen that the pre-calculated value will be recalculated, which is purely an overhead.
Refer to the diagram below for the clear picture:
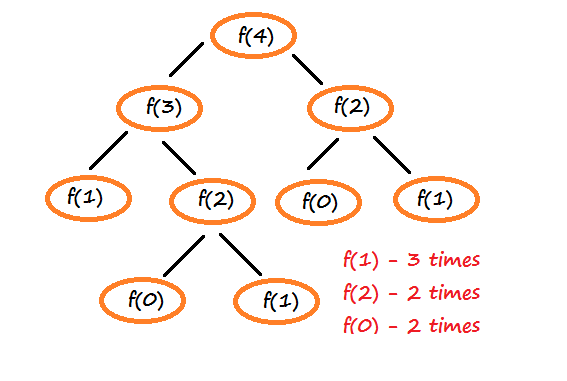
Here f(1), f(2), and f(0) are being computed multiple times and are termed as overlapping sub-problems (i.e. repetitive sub-problems).
It would have been better, if we have stored their result (when they were computed for the first time) in an array and reused them when the recalculation was needed.
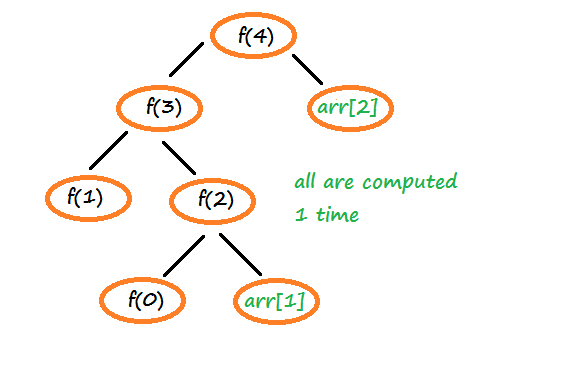
This approach of storing the solutions of the overlapping sub-problems for later use is called memoization (not memorize).
Here is the modified example, where we are storing the solutions of the repetitive sub-problems (e.g. f(1), f(2), & f(0)) of the Fibonacci series into an array:
#include <iostream>
#include<algorithm> //for the fill() method
using namespace std;
//array for memoization (to store solutions of sub-problems)
int memoize[100];
//method to find nth fibonaacci number using DP
int fibonaaciDP(int n){
//if the value already exists in the memoization array, return it
if(memoize[n] != -1) return memoize[n];
//otherwise recursively compute (also store) and return the result
memoize[n] = fibonaaciDP(n-1) + fibonaaciDP(n-2);
return memoize[n];
}
int main(){
//fill the array with -1
fill(memoize, memoize+100, -1);
//store the starting values of the fibonaaci series (i.e. a=0 & b=1)
memoize[0] = 0;
memoize[1] = 1;
//find the nth fibonacci number using the fibonaaciDP(n) method
cout << fibonaaciDP(15); #outputs 610
return 0;
}610 is the 15th Fibonacci number (Considering 0 as zeroth number :P).
In this example, we are first checking if the nth number of the Fibonacci series exists in the memoize array.
If so, we use its value otherwise we recursively compute it and return the result after storing the same in the array.
In this approach, the program never recalculates the same result instead, it reuses them by storing the sub-solutions in an array.
This approach of solving a problem by memorizing the solutions of the sub-problems is known as dynamic programming.
What are the benefits of Dynamic Programming?
Solving a problem by reusing the solutions which have been computed before reduces the total computations of the program.
It executes code faster than code that has not taken advantage of dynamic programming.
If we test our previous examples with a large value of N, we will notice the difference in time taken by each approach to give the final result.
When to use Dynamic Programming?
We cannot solve every problem using the logic of dynamic programming.
We can implement dynamic programming only in those cases where we can divide the problem into overlapping sub-problems e.g. the rod cutting problem, 0-1 knapsack problem, etc.
As in our previous example, the sub-problems such as f(0), f(1), and f(2) were recomputed when we used the recursive approach to get the 4th Fibonacci term.
Dynamic Programming vs Divide and Conquer
Dynamic programming and Divide & Conquer algorithm are two different approaches to solve any problem.
The divide and conquer method is used when problems can be solved by combining optimal solutions to non-overlapping sub-problems. Examples: merge sort, quick sort, etc.
Whereas dynamic programming is used in those problems which have the scope of computing similar subproblems again and again.
When to use whom:
Overlapping subproblems -> Dynamic Programming
Non Overlapping subproblems -> Divide and Conquer method
Sometimes we may require to use both the algorithms together to solve a particular problem.
For instance, in the above example, we have implemented both dynamic programming along with the divide & conquer method to solve the nth Fibonacci number problem.
In this tutorial, we learned the concept of dynamic programming with an example. We learned how dynamic programming can make algorithms more time-efficient when there is a possibility of reusing the solution of the subproblems.
the contents are really amazing.
thanks to you.