Summary: In this tutorial, we will learn What is 0-1 Knapsack Problem and how to solve the 0/1 Knapsack Problem using Dynamic Programming.
Introduction to 0-1 Knapsack Problem
https://en.wikipedia.org/wiki/Knapsack_problem
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible
For example, consider we are given the following 4 weights with respective values.
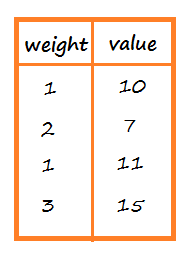
We are also given a knapsack bag that has a total weight limit of 5.
We have to find the number of each weight to include in the bag so that the total weight is less than or equal to 5 and the total value is as large as possible.
Note: We cannot include the faction of the item, we either include the whole single item or not.
There are multiple ways to solve the 0-1 Knapsack problem, one such method is recursion.
0-1 Knapsack Solution using Recursion (Inefficient Approach)
For each item, we have to decide whether to include it in the knapsack bag.

To make this decision, we compare the total value of the bag when including the item with the value when not including the item.
Since for every item we have to repeat the same process, we use recursion.
#include <iostream>
//Weights
int weight[] = {0, 1, 2, 1, 3};
//values
int value[] = {0, 10, 7, 11, 15};
//recursive funciton
int knapsack(int n, int KW){
//base condition
if(n<=0 || KW<=0)
return 0;
//don't select item if its weight is greater than knapsack weight
else if(weight[n]>KW)
return knapsack(n-1, KW);
//check which gives more value
//1. When not including the nth item
//2. When including the nth item
else{
//total value when not including the item
int not_include_nth_item = knapsack(n-1, KW);
//total value when including the item
int include_nth_item = value[n] + knapsack(n-1, KW-weight[n]);
//return the larger value
return std::max(not_include_nth_item, include_nth_item);
}
}
//Driver code
int main() {
//knapsack(<number_of_items>, <knapsack_weight>)
std::cout << knapsack(4, 5);
}The above program has two successive recursive calls within the function:
- knapsack(n-1, KW) – Total value when not including the nth item.
- knapsack(n-1, KW – weight[n]) – Total value when including the nth item.
This exponentially increases the time complexity of the program to O(2n).
We can definitely improve the efficiency of our program by incorporating other techniques.
The 0-1 Knapsack problem can be solved using the greedy method however using dynamic programming we can improve its efficiency.
0-1 Knapsack Solution using Dynamic Programming
The idea is to store the solutions of the repetitive subproblems into a memo table (a 2D array) so that they can be reused i.e., instead of knapsack(n-1, KW), we will use memo-table[n-1, KW].
But, what is the subproblem here?
For instance, when deciding on the 4th item (whether to include it or not) we recursively make decisions for all the preceding items (i.e., 3rd, 2nd, and 1st items) twice.
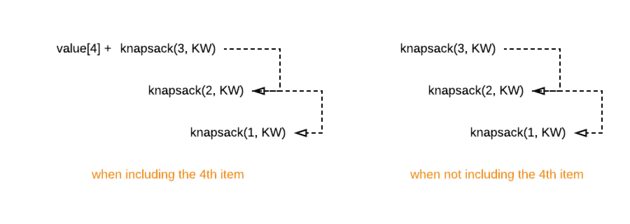
When deciding on the 3rd item, the decisions of the preceding items are made once again, although they were computed initially while making the decision for the 4th item.
This computation of the maximum value for the nth item is the subproblem here, which is computed repeatedly.
When calculated for the first time we store the corresponding value of Knapsack(N-1, KW) into the memo table and reuse if needed
Now the question arises, how the memo table will look like or supposed to have?
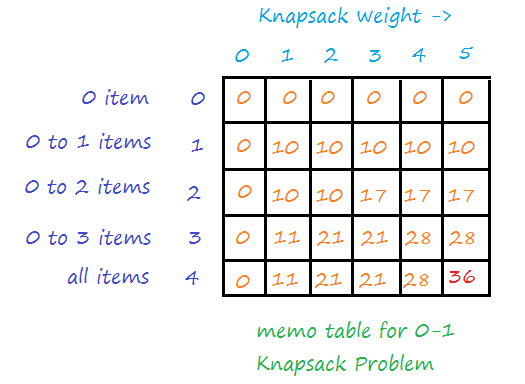
Note: The size of the memo table is (Total number of items + 1) * (Knapsack Weight+1).
In the memo table:
- Row – is the number of items we can take. The first row is 0, it means no item is available. The second row is 1, it means only the 1st item is available. Similarly, Third-row is 2, it means only 1st and 2nd item are available…Forth row tells that all 4 items should be considered for computing the total value for the given knapsack weight.
- Column – is the knapsack weight. The first column is 0, it means the knapsack bag is not available. The second column is 1. it means the value of knapsack weight is 1, therefore we can only take those items whose total weights sum up to 1. The fourth column (Last column) is 5, which is what we want, the total weight in the knapsack bag.
Each table cell stores the solution of a subproblem. For instance, memo-table[3][2] = 21 means for a knapsack bag of weight equal to 2, the maximum value that can be achieved with the first 3 items is 21.
As we have a memo table available with us, we iterate through its cells and use the previously stored values to calculate the values for the current cell.
Here is the implementation of the discussed dynamic programming solution:
C++
#include <iostream>
#define MAX 200
using namespace std;
//weights
int weight[] = {0, 1, 2, 1, 3};
//values
int value[] = {0, 10, 7, 11, 15};
//knapsack bag weight limit
int knapsack_weight = 5;
//count of items
int n = 4;
class KnapsackDP{
public:
int **memoTable;
KnapsackDP(){
// memo table
this->memoTable = new int*[n+1];
//Initiale each cell with 0
for(int i=0; i<n+1; i++){
this->memoTable[i]= new int[knapsack_weight+1] {0};
}
}
int solve(){
//Compute and fill the memo table
for(int i=1; i< (n + 1); i++){
for(int j=1; j<(knapsack_weight + 1); j++){
//when not including the item
int not_taking_item = memoTable[i-1][j];
//when including the item
int taking_item = 0;
if(weight[i] <= knapsack_weight){
if(j-weight[i] < 0)
taking_item = memoTable[i-1][j];
else
taking_item = value[i] + memoTable[i-1][j-weight[i]];
}
//store the larger value in the table
memoTable[i][j] = max(not_taking_item, taking_item);
}
}
//return the max value for the given knapsack weight
return memoTable[n][knapsack_weight];
}
//Function output the included items
void selected_items(){
for(int i=n, j= knapsack_weight; i>0; i--){
if(memoTable[i][j] != memoTable[i-1][j]){
cout << "Item: "<<i <<" Selected \n";
j = j- weight[i];
}
}
}
};
int main()
{
KnapsackDP kdp;
cout << "Total Benefit: "<< kdp.solve() <<endl;
//To print which items are included
kdp.selected_items();
return 0;
}Java
public class Main{
public static void main(String args[]){
//weights
int weight[] = {0, 1, 2, 1, 3};
//values
int value[] = {0, 10, 7, 11, 15};
//Taking Knapsack weight as 5
KnapsackDP kdp = new KnapsackDP(5, 4, weight, value);
System.out.println("Total Benefit: "+kdp.solve());
//To print which items are selected
kdp.selected_items();
}
}
class KnapsackDP{
int knapsack_weight;
int n;
int weight[];
int value[];
int memoTable[][];
public KnapsackDP(int W,int N,int weight[],int value[]){
this.knapsack_weight = W;
this.n = N;
this.weight = weight;
this.value = value;
this.memoTable = new int[N+1][W+1];
}
public int solve(){
//compute and fill the table
for(int i=1; i< (n + 1); i++){
for(int j=1; j<(knapsack_weight + 1); j++){
//when not including the item
int not_taking_item = memoTable[i-1][j];
//when including the item
int taking_item = 0;
if(weight[i] <= knapsack_weight){
if(j-weight[i] < 0)
taking_item = memoTable[i-1][j];
else
taking_item = value[i] + memoTable[i-1][j-weight[i]];
}
//store the larger value in the memo table
memoTable[i][j] = Math.max(not_taking_item, taking_item);
}
}
//return the max value for the given knapsack weight
return memoTable[n][knapsack_weight];
}
//Function to output included items
public void selected_items(){
for(int i=n, j= knapsack_weight; i>0; i--){
if(memoTable[i][j] != memoTable[i-1][j]){
System.out.println("Item: "+i+" Selected");
j = j- weight[i];
}
}
}
}The time complexity of the program is O(n2) i.e, much better than the recursive solution.
How to know which item is included in the bag?
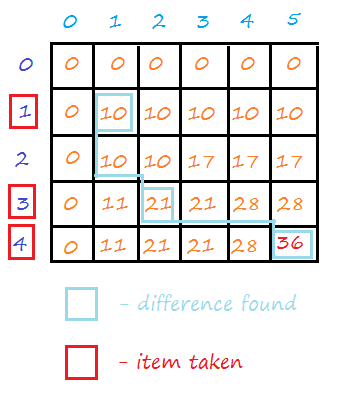
To know which item is selected for calculating total Benefit/Value, start from the last row and column index.
Go one level up and check whether the value in the upper level is smaller or not.
if(memoTable[i][j] != memoTable[i-1][j])- If YES, then it means that the difference is caused because of including the last item (4th item in our case). Now subtract the weight of the last (selected) item from j and repeat the same process for the resultant value of the jth column.
- If NO, then go one level up more and check for the difference in the value. Keep going up until you see the difference in the value.
Output:
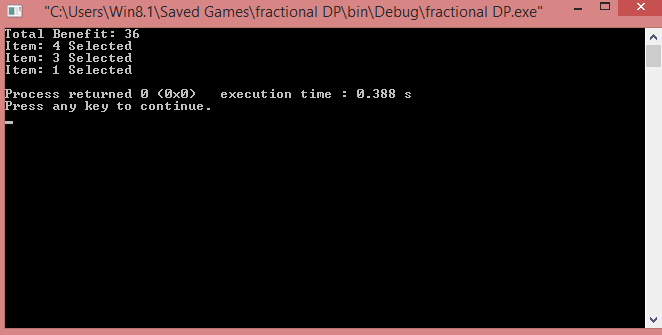
In this tutorial, we learned to solve the 0-1 knapsack problem using the dynamic programming algorithm in C++ and Java programming languages.