Breadth-First Search in Python [Full Code]

Summary: In this tutorial, you will learn to implement the breadth first search (BFS) in Python with the help of an example.

What is Breadth-First Search?

Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.

The basic idea of the breadth-first search algorithm is to explore all the nodes at the current depth level before moving on to the next level.

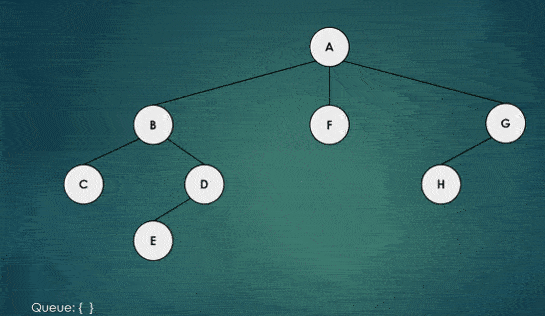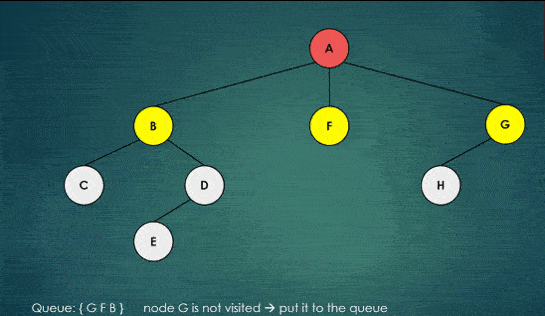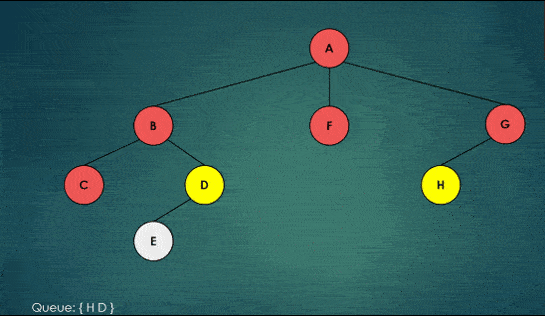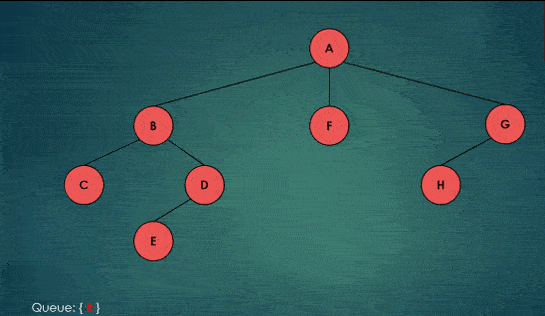
To do this, the algorithm uses a queue data structure, which follows the principle of first-in, first-out (FIFO). The algorithm starts by putting the root node in the queue, and then takes the first node out of the queue.

It then adds all of the unvisited neighbors of this node to the queue, and marks the current node as visited. This process is repeated until the queue is empty.

BFS can be used for different goal, one common use case is finding the shortest path between two nodes on a unweighted graph, another one is traversing all the nodes in the graph in order to build a map of the graph or test if the graph is connected.

BFS in Python

function BFS(graph, start_node)
    create a queue and add the start_node to it
    create a set to store visited nodes and add the start_node to it

    while the queue is not empty
        dequeue a node from the front of the queue
        for each unvisited neighbor of this node
            mark the neighbor as visited
            add the neighbor to the queue

The pseudocode describes the main steps and logic of the algorithm. In the first step, it creates a queue and adds the starting node to it. It also creates a set to store the visited nodes, and adds the starting node to it as well.

Next, it enters into a while loop which keeps running as long as there are still nodes in the queue. Inside the while loop, it dequeues a node from the front of the queue and examines each of its unvisited neighbors.

For each unvisited neighbor, it marks the neighbor as visited and adds it to the queue. This process continues until all the nodes have been visited.

Here’s an example of how you can implement BFS on a graph in Python:

from collections import defaultdict, deque

def bfs(graph, start_node):
    """
    Perform breadth-first search on the given graph, starting from the start_node.
    Returns a list of nodes in the order that they were visited.
    """
    # Create a queue for BFS
    queue = deque([start_node])
    # Create a set to store visited nodes
    visited = set([start_node])

    # Traverse the graph
    while queue:
        # Dequeue a vertex from queue and print it
        node = queue.popleft()
        print(node, end=' ')

        # Get all adjacent vertices of the dequeued vertex
        # If a adjacent has not been visited, then mark it
        # visited and enqueue it
        for neighbour in graph[node]:
            if neighbour not in visited:
                visited.add(neighbour)
                queue.append(neighbour)

# Define the graph as a dictionary, where each key is a node
# and the value is a list of its neighbors
graph = defaultdict(list)
graph[0] = [1, 2]
graph[1] = [2]
graph[2] = [0, 3]
graph[3] = [3]

# Perform BFS, starting at node 0
bfs(graph, 0)

In this example, the input graph is represented as a dictionary, where the keys are the nodes, and the values are lists of the node’s neighbors.

The bfs function takes two arguments: the graph and the starting node. The function uses a queue to store the nodes that need to be visited, and a set to keep track of the nodes that have already been visited.

The function starts by adding the starting node to the queue, and then repeatedly dequeues a node from the front of the queue, prints it, and enqueues all of its unvisited neighbors.

This example implementation will print out the node visit order as it visits them in BFS order, you can use this as a starting point and adapt it for your specific use case

This is just an example, you can use different data structure to represent the graph and use other properties of the nodes and edges to store information.

Advantages and Disadvantages of BFS

One of the main advantages of BFS is that it guarantees that the shortest path will be found, because it explores all the nodes at the current depth level before moving on to the next level, which means that it will always discover the goal node that is closest to the start node first.

The major disadvantage of BFS is its memory requirement, as it needs to keep track of all the nodes at the current depth level in the queue, which can be a problem if the tree or graph is very large.