Summary: In this tutorial, we will learn what In-order Traversal is and how to implement In-order traversal to traverse a graph in C++ and Java.
Introduction to Inorder Traversal
A binary tree can be traversed in 2 major ways and they are:
Inorder traversal is a type of Depth-first traversal which traverse a graph in the following fashion:
- Left Subtree
- Root
- Right Subtree.
For example, consider the inorder traversal of the following graph:
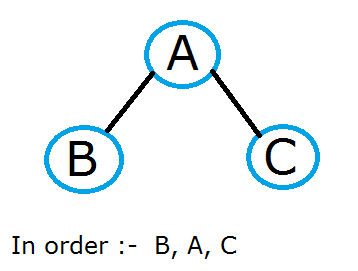
In this example, the algorithm visits the left node first i.e. B then the root node i.e. A, and finally the right node i.e. C.
Since In-order traversal is Depth First Search (because it explores depth along a branch), it can be implemented using a stack.
But the best way to implement an In-order traversal algorithm is using recursion because recursion implements stack and makes backtracking very easy.
Inorder Traversal Recursive Algorithm
- Inorder(leftChild)
- Output(currentNode)
- Inorder(rightChild)
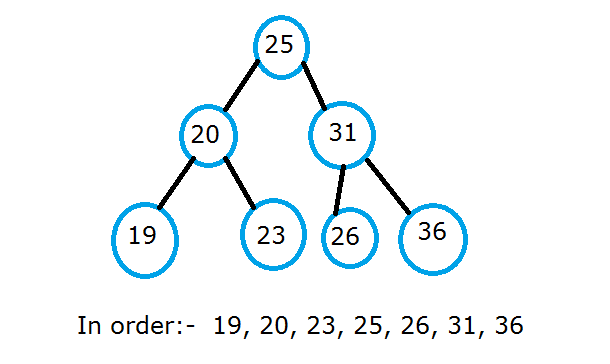
Here is the implementation of the Inorder traversal algorithm in C++ and Java.
C++
#include <iostream>
using namespace std;
//Class TreeNode represent each node
class TreeNode{
public:
int data;
TreeNode *leftNode {nullptr};
TreeNode *rightNode {nullptr};
TreeNode();
TreeNode(int d);
void insertData(int d);
void inorderTraverse();
};
//Implementing TreeNode class prototypes function.
TreeNode::TreeNode(int d){
data = d;
}
//Function to insert data into binary search tree
void TreeNode::insertData(int d){
if(d < data){
if(leftNode == nullptr){
leftNode= new TreeNode(d);
} else {
leftNode->insertData(d);
}
} else {
if(rightNode == nullptr){
rightNode = new TreeNode(d);
} else {
rightNode->insertData(d);
}
}
}
//Inorder traversal algorithm using Recusrion
void TreeNode::inorderTraverse(){
if(leftNode != nullptr){
leftNode->inorderTraverse();
}
cout << data << ", ";
if(rightNode != nullptr){
rightNode->inorderTraverse();
}
}
int main()
{
//Taking root node as 25
TreeNode *root= new TreeNode(25);
//inserting data into the binary tree
root->insertData(20);
root->insertData(23);
root->insertData(31);
root->insertData(36);
root->insertData(19);
root->insertData(26);
//Calling inorder traversal function from root object
root->inorderTraverse();
return 0;
}Java
class Node{
int value;
Node left;
Node right;
//Constructor to initialize value to node
Node(int value){
this.value = value;
left = right = null;
}
//Function to insert data into binary search tree
public void insert(int v){
if(v < value){
if(left == null){
left = new Node(v);
} else {
left.insert(v);
}
} else {
if(right == null){
right = new Node(v);
} else{
right.insert(v);
}
}
}
//In-Order Travesal
Algorithm using Recusrion
public void inOrder(){
if(left != null){
left.inOrder();
}
System.out.print(value+" ");
if(right != null){
right.inOrder();
}
}
}
class Main {
public static void main(String[] args) {
Node root = new Node(25);
root.insert(20);
root.insert(31);
root.insert(19);
root.insert(23);
root.insert(26);
root.insert(36);
root.inOrder();
}
}Output
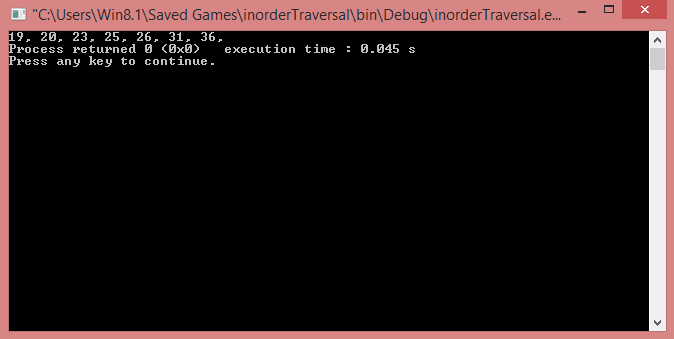
Notice the output of the program, It is in ascending order.
It is because the Inorder traversal of a Binary Search Tree always yields the nodes in increasing order.
In our program, we have written the insert function in such a way that it forms a Binary Search Tree (In BST, a node have maximum 2 child nodes: left child node with a smaller value, and right child node with greater value).
In this tutorial, we learned what In-order traversal is and have also seen the implementation of In-order travseral to traverse a binary search tree in C++ and Java.