Summary: In this post, we will learn how to solve the Coin Change problem using Dynamic Programming in C, C++, and Java.
What is Coin Change Problem?
Given a set of Coins for example coins[] = {1, 2, 3} and total amount as sum, we need to find the number of ways the coins[] can be combined in order to get the sum, abiding the condition that the order of the coins doesn’t matter.
Example:
- coins[] = {1, 2, 3}
- sum = 4
- Possible changes: {1,1,1,1}, {2,2}, {1,3}, {1,1,2}.
- Solutions: 4
Note: The order of coins does not matter – For example, {1,3} = {3,1}.
The Coin Change Problem can be solved in two ways –
- Recursion – Naive Approach, Slow.
- Dynamic Programming – Efficient Approach, Fast.
Let’s see the recursive way to solve the coin change problem and study its drawbacks.
Coin Change Problem Solution using Recursion
For every coin, we have two options, either to include the coin or not.
When we include the coin we add its value to the current sum solve(s+coins[i], i) and if not then simply move to the next coin i.e. next recursive call solve(s, i++).
Here is the recursive solution of the coin change problem in C and Java.
C
#include <stdio.h>
int coins[] = {1,2,3};
int numberOFCoins = 3, sum = 4;
int solve(int s, int i){
if(numberOFCoins == 0 || s > sum || i>=numberOFCoins)
return 0;
else if(s == sum)
return 1;
return solve(s+coins[i],i) + solve(s,i+1) ;
}
int main()
{
printf("Total solutions: %d",solve(0,0));
return 0;
}Java
class CoinChange{
int coins[], sum;
CoinChange(int coins[], int sum){
this.coins = coins;
this.sum = sum;
}
public int solve(int s, int i){
if(coins.length == 0 || s > sum || i>=coins.length)
return 0;
else if(s == this.sum)
return 1;
return solve(s+coins[i],i) + solve(s,i+1) ;
}
}
public class Main
{
public static void main(String[] args){
int coins[] = {1,2,3};
CoinChange coinchange = new CoinChange(coins,4);
System.out.println("Total solutions: "+coinchange.solve(0,0));
}
}Output
Total solutions: 4The following picture depicts the recursive calls made in the execution of the program.
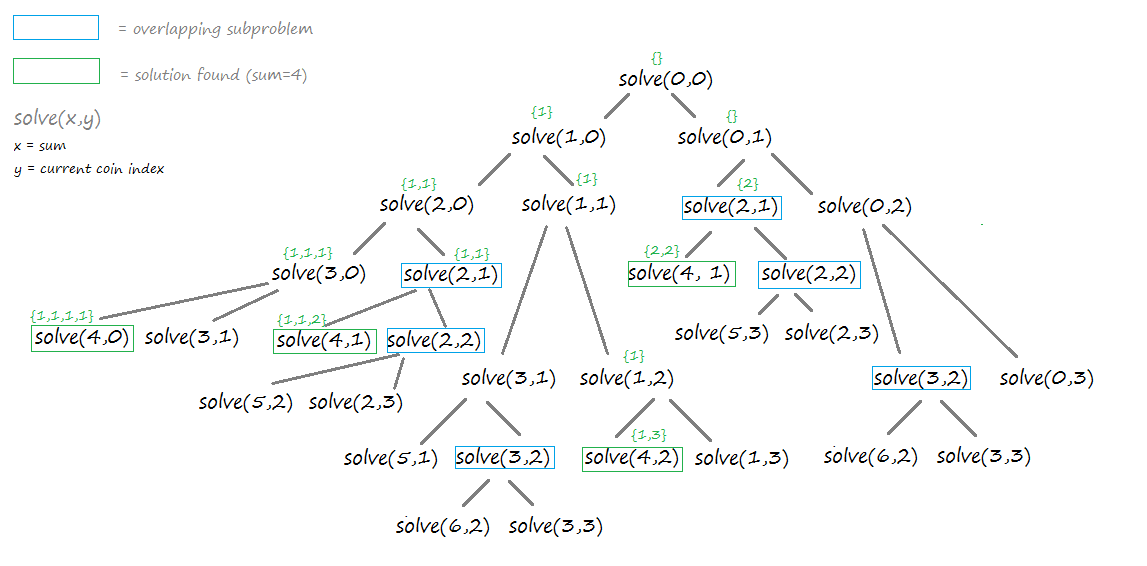
- Problems: Time complexity + Overlapping subproblems
- Exponential time complexity: O(2n), where n is the number of coins
Clearly, in the recursive method, the algorithm is unnecessarily calculating the same subproblems multiple times. We can use Dynamic Programming to solve the coin change problem in an efficient way.
The dynamic approach to solve the coin change problem is similar to the solution of 01 Knapsack problem using dynamic programming.
Let’s see how can we can solve the coin change problem using DP.
Coin Change Problem Solution using Dynamic Programming
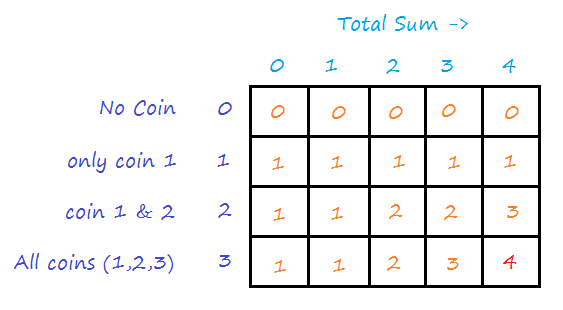
We need to use a 2D array (i.e memo table) to store the subproblem’s solution. Refer to the picture below.
Note:
- Size of dpTable is (number of coins +1)*(Total Sum +1)
- First column value is 1 because if total amount is 0, then is one way to make the change (we do not include any coin).
- Row: Number of coins. The 1st-row index is 0 means no coin is available. 2nd row is 1, it means only 1st coin is available, similarly, the 3rd-row value index is 2 means the first two coins are available to make to the total amount and so on.Row index represent index of coin in coins array not the coin value.
- Coulmn: Total Amount (sum). The 1st-column index is 0, it means sum value is 0. 2nd column index is 1 therefore combination of coins should make the sum of 1, similarly, 3rd column value is 2, means change of 2 is required and so on.
Thus each table field is storing the solution of subproblems. For Example, dpTable[2][3]=2 means there are 2 ways to get the sum of 3 using the first two coins {1,2}.
The last column and last row value will give the final result.
Here We need to loop through all the indexes (except 1st row and 1st column) in the memo table and make use of previously stored solutions of the subproblems.
- If coin value is greater than the dpSum, then do not consider the coin i.e
dpTable[i][j]=dpTable[i-1][j]. - If coin value is smaller than the dpSum we can consider the coin i.e
dpTable[i][j]=dpTable[i-1][dpSum]+dpTable[i][j-coins[i-1]].
Let’s implement the same in our program.
C
#include <stdio.h>
int coins[] = {1,2,3}, sum=4;
int numberOfCoins = 3;
//Function to initialize 1st column of dpTable with 1
void initDpTable(int dpTable[][sum+1]){
int i;
//First row to 0
for(i=1; i<=sum+1; i++){
dpTable[0][i] = 0;
}
//First column to 1
for(i=1; i<=numberOfCoins; i++){
dpTable[i][0] = 1;
}
}
int solve(int dpTable[][sum+1]){
int coinIndex, dpSum;
for(coinIndex=1; coinIndex<numberOfCoins+1; coinIndex++){
for(dpSum=1; dpSum< sum+1; dpSum++){
//coin value should be less than or equal to sum value in order to consider it
if(coins[coinIndex-1] > dpSum)
dpTable[coinIndex][dpSum] = dpTable[coinIndex-1][dpSum];
else
dpTable[coinIndex][dpSum] = dpTable[coinIndex-1][dpSum]+dpTable[coinIndex][dpSum-coins[coinIndex-1]];
}
}
//return final row and column value
return dpTable[numberOfCoins][sum];
}
int main()
{
int dpTable[numberOfCoins+1][sum+1];
initDpTable(dpTable);
printf("Total Solutions: %d",solve(dpTable));
return 0;
}Java
class CoinChange{
int coins[], sum;
int dpTable[][];
CoinChange(int coins[], int sum){
this.coins = coins;
this.sum = sum;
this.dpTable = new int[coins.length+1][sum+1];
initDpTable();
}
//Function to initialize 1st column of dpTable with 1
private void initDpTable(){
for(int i=1; i<coins.length; i++){
dpTable[i][0] = 1;
}
}
public int solve(){
for(int coinIndex=1; coinIndex<coins.length+1; coinIndex++){
for(int dpSum=1; dpSum< sum+1; dpSum++){
//coin value should be less than or equal to sum value in order to consider it
if(dpSum-coins[coinIndex-1] < 0)
dpTable[coinIndex][dpSum] = dpTable[coinIndex-1][dpSum];
else
dpTable[coinIndex][dpSum] = dpTable[coinIndex-1][dpSum]+dpTable[coinIndex][dpSum-coins[coinIndex-1]];
}
}
//return final row and column value
return dpTable[coins.length][sum];
}
}
public class Main
{
public static void main(String[] args){
int coins[] = {1,2,3};
CoinChange coinchange = new CoinChange(coins,4);
System.out.println("Total solutions: "+coinchange.solve());
}
}Output
Total Solutions: 4Overview
- Time Complexity: O(numberOfCoins*TotalAmount)
- Space Complexity: O(numberOfCoins*TotalAmount)
In this tutorial, we learned to what is coin change problem and how to solve coin change problem using dynamic programming in C and Java.