The shortest path algorithms such as Dijkstra and Bellman-Ford algorithm don’t give the right results when there’s a negative cycle in the graph.
| Dijkstra’s Algorithm | Bellman-Ford Algorithm | |
|---|---|---|
| Graph with Negative Edge | Fails | Pass |
| Graph with Negative Cycle | Fails | Fails |
Recommended read: Why doesn’t Dijkstra’s algorithm work in graphs with negative-weighted edges?
Although Bellman-Ford works with negative edges, it still fails to deliver the correct results (i.e. the shortest route) in case of the graphs with negative cycles.
Consider the following graph with a negative cycle:
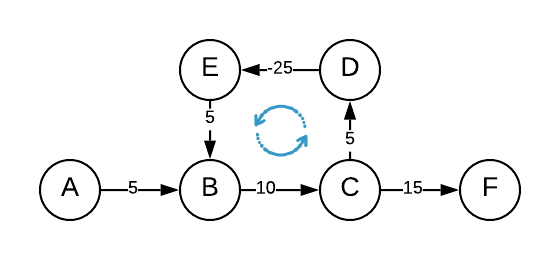
What do you think is the shortest route from A to F?
You may say A->B->C->D->E->B->C->F (Distance = 15), but that’s not correct..
The answer is that no optimal path exists from A to F due to the presence of a negative cycle.
The overall distance of the cycle B->C->D->E->B is -5. The more we repeat the cycle, the more the distance of the path decreases i.e. A->(B->C->D->E->B)n-times->C->F (Distance = -∞).
That’s why most of the algorithms run into ambiguity while dealing with negative cycles and fail as a result.
In such cases, it’s best to use the Bellman-Ford algorithm. It may not get results but can detect negative cycles.
I hope now it is clear to you now, how negative cycles causes the algorithm to fail to calculate the shortest path in a given graph.